Question

Помогите пожалуйста
Вычислить объем тела, образованного вращением вокруг оси ОХ фигуры, ограниченной параболами y=x² и y=2√x

Answer 1

Дано: Y₁(x) = x², Y₂(x) = 2*√x.

Найти: V = ? - объём тела вращения.

Думаем: Формула вычисления объёма тела вращения вокруг оси ОХ:  $V = pi intlimits^a_b {Y(x)^2} , dx$

Пошаговое объяснение:

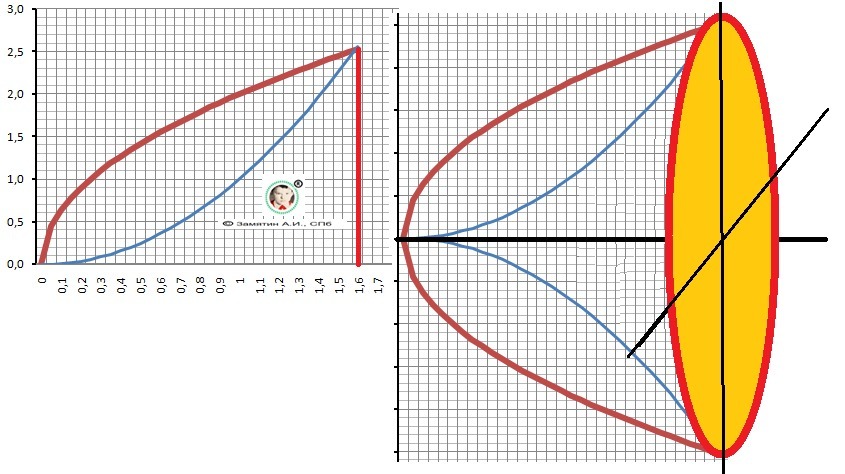
Рисунок с графиками функций и условное изображение фигуры - в приложении.

1. Находим пределы интегрирования -  точки пересечения графиков.

2√x = x²,   4x = x⁴,   x³ = 4 x = ∛4 = a - верхний предел.

b = 0 - нижний предел. Вычисляем объём фигур по каждой функции, а затем найдём разность объёмов.

$V_{1}=pi intlimits{(sqrt{x})^2 } , dx=pi intlimits^a_b {x} , dx=pi frac{x^2}{2}$

V = π*a/2 = 0.7937

$V_{2}=pi intlimits{(x^2)^2} , dx=pi frac{x^5}{5}$

V₂ =  a⁵/5

Формулы записали - остаётся вычислить разность разностей.

V1(b) = 0

V1(a) = π*a/2 =  1/2*π*∛4 - объем под графиком корня.

V2(b) = 0

$V_{2}(sqrt[3]{4}) = pifrac{sqrt[3]{4}^5}{5}=pifrac{sqrt[3]{x^!0} }{5}}=pifrac{8}{5}sqrt[3]{2}$ - объём под параболой.

V1 = 1.26*π и V2 = 2.016*π

И находим разность объёмов.

Что-то трудно и прочитать формулы и записать их. Возможны опечатки.