Question

Докажите что при любых значениях a трёхчлен 4а² - 12а+17 принимает положительные значения

Answer 1

4а² - 12а+17 - возрастающая парабола, ветви которой направленны вверх

найдем координаты вершины:

x = -b/2a

x = 12/8 = 1,5

y = 4x² - 12x+17 = 4*1,5² - 12*1,5+17 = 8

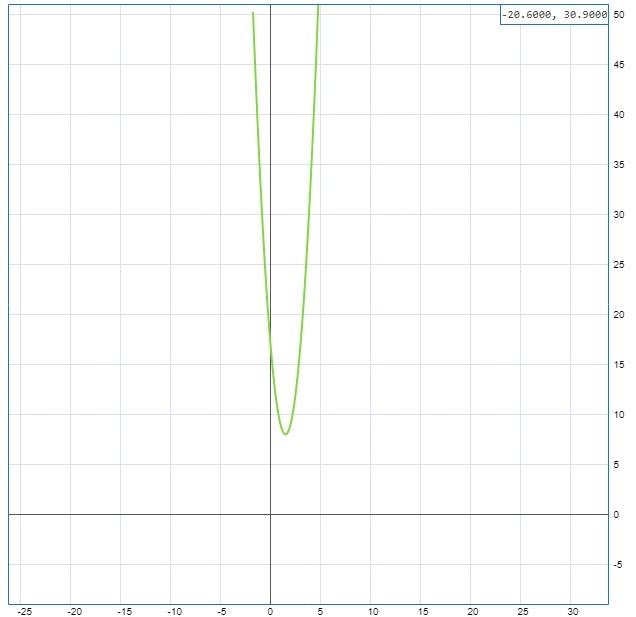
Т.к вершина параболы (1.5;8) и она возрастающая, значение 4а² - 12а+17 будет положительно при любом а

Дополнительно можешь начертить график  y = 4x² - 12x+17, для наглядности

Answer 2

$4a^2-12a+17\\D=12^2-4cdot 4cdot 17=144-272=underline {-128<0}; ; Rightarrow \\4a^2-12a+17>0; ; pri; ; ain R$