В четырех угольнике ABCD BC || AD . Биссектриса угла BAD пересекает сторону BC в точке K. Докажите,что треугольник ABK - равнобедренный. 50 БАЛЛОВ
Ответы
Ответ дал:
0
Угол ВАК равен углу КАД так как АК биссектрисса
Угол КАД равен углу ВКА при АД параллельно ВС и секущей АК отсюда следует что угол ВКА равен углу АКВ отсюда следует треугольник АВК равнобедренный
Ч.Т.Д
Ответ дал:
0
Это конечно необязательно,но можно рисунок?
Ответ дал:
0
∠ВКА =КАД - как накрест лежащие при двух параллельных АД и ВС и секущей АК, но ∠КАД=∠ВАК⇒∠ВАК=∠ВКА, а раз углы при основании равны, то такой треугольник равнобедренный.
Приложения:
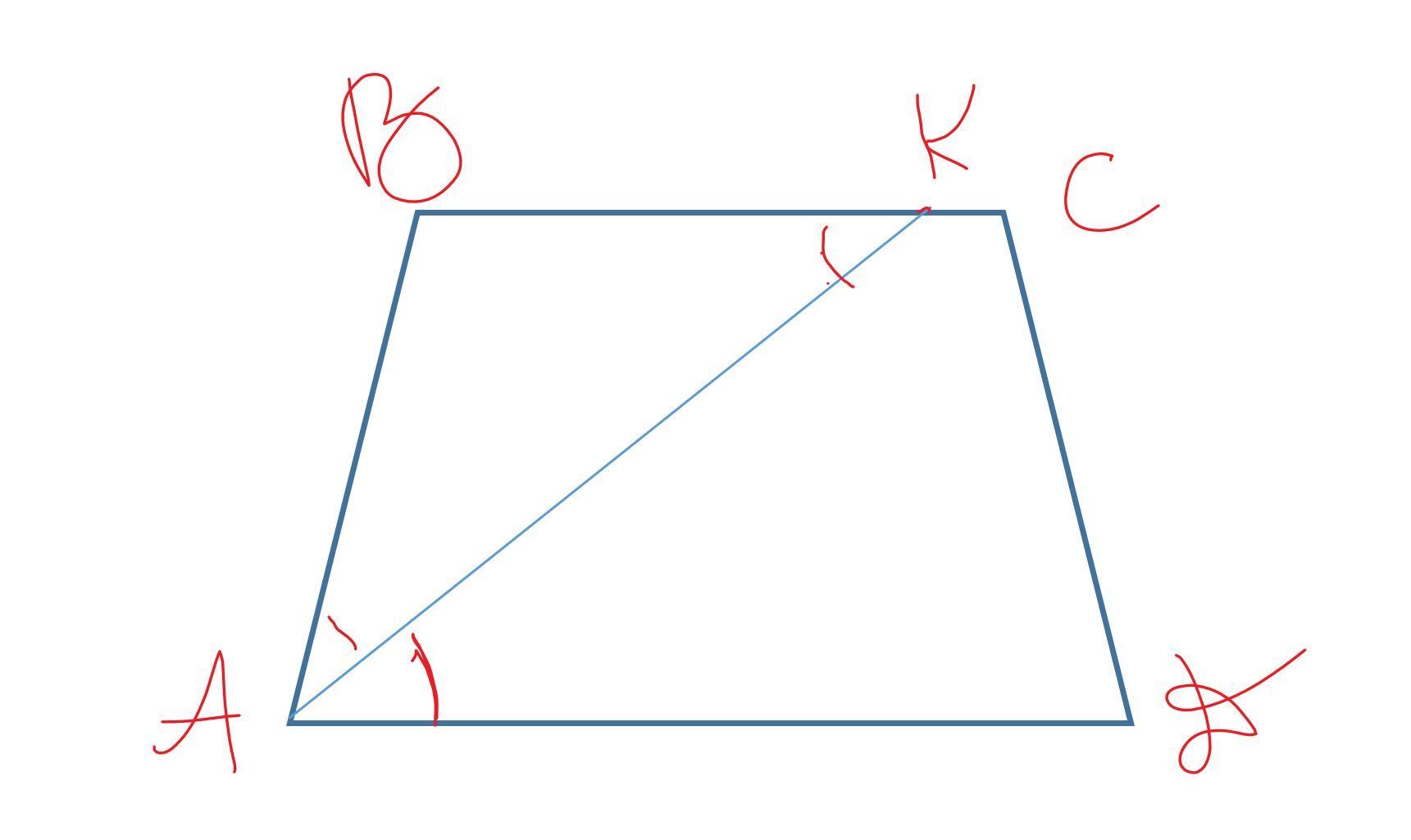
Ответ дал:
0
Пока писала, кто-то уже ответил, удали тогда мок решение, чтобы баллы вернуть.
Вас заинтересует
2 года назад
3 года назад
9 лет назад
10 лет назад