Question

найдите длину окружности описанной около квадрата со стороной 12 см

Answer 1

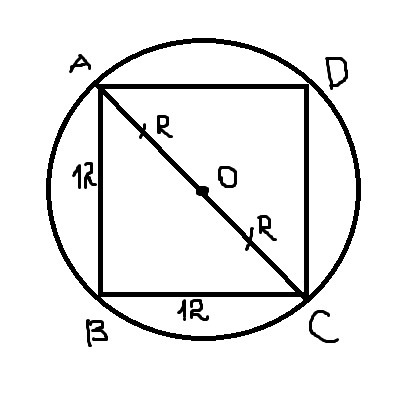
Дано: ABCD - квадрат.

AB=BC=CD=AD=12 см

Найти: l - длина окружности

Решение:

1) l = 2$pi$R=$pi$D, где D - диаметр окружности.

Диаметр окружности есть диагональ квадрата, вписанная в эту окружность.

2) треуг. ABC - прямоугольный, равнобедренный.

(можно через теорему косинусов, можно через Пифагора.)

По теореме Пифагора:

$AC^2 = AB^2+BC^2\AC=sqrt{AB^2+BC^2}\ AC = sqrt{144+144}=sqrt{288}=12sqrt{2}$

3) $l = pi D=12pi sqrt{2}$

Ответ: $l=12pi sqrt{2}$