Question

Розв'яжіть графічну систему рівнянь
y-x2+4x=0
x-y=6

Answer 1

$left { {{y=x^2-4x} atop {y=x-6}} right. \left { {{y=(x-2)^2-4} atop {y=x-6}} right.$

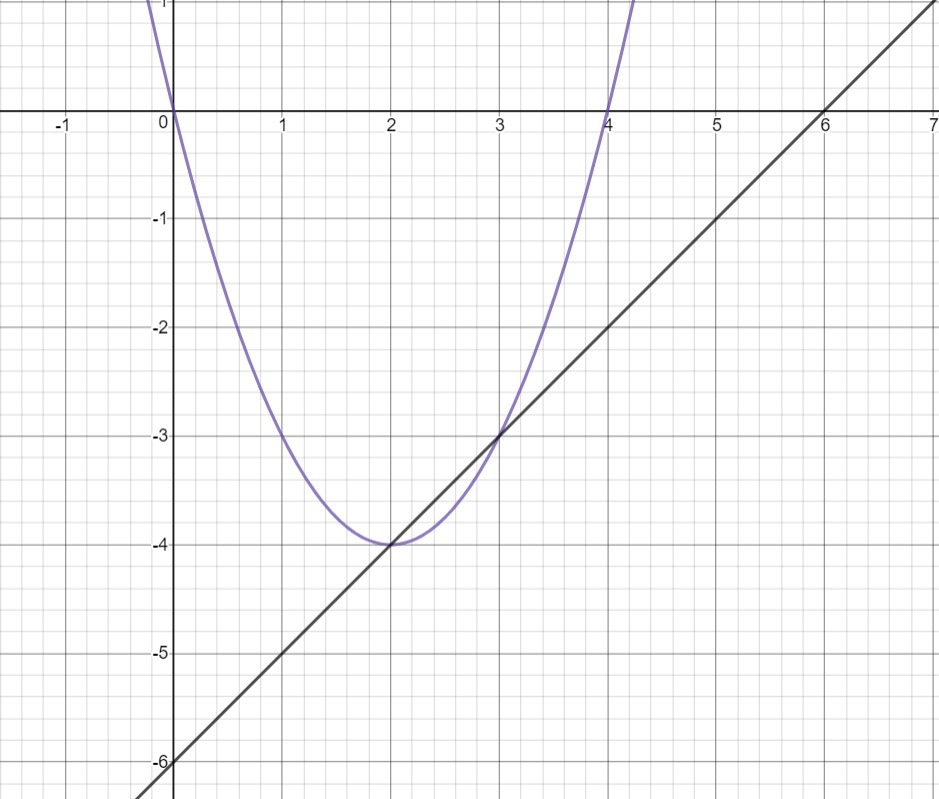
Первое уравнение это парабола ветви которой направлены вверх, координаты вершины (2;-4) и пересекает оси в точках:

$y(0)=0^2+4*0=0\x(0): x-2=б2\left[begin{array}{ccc}x=0\x=4\end{array}$

Второй график это прямая, которая составляет 45° с осью x и пересекает оси в точках:

$y(0)=0-6=-6\x(0): 6$

Система имеет решение когда:

$x^2-4x=x-6;\x^2-5x+6=0; D=25-24=1;\x=frac{5б1}{2} \left[begin{array}{ccc}x=2\x=3\end{array}$

f2(2)=2-6= -4

f2(3)=3-6= -3

Ответ: (2;-4) и (3;-3)