Question

90 БАЛЛОВ!
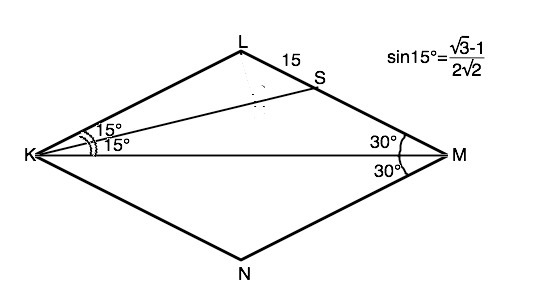
В ромбе KLMN KS – биссектриса угла MKL, угол LKN равен 60°, LS = 15 см. Найдите площадь ромба KLMN

Answer 1

  Диагонали ромба - биссектрисы его углов. Сумма углов параллелограмма, прилежащие одной стороне, равна 180°.  Угол LKN=60°, поэтому угол КLS=120°, а угол LKM=30°. Угол LKS=0,5•∠LKM=15° ( т.к. KS- биссектриса). Из суммы углов треугольника угол КSL=45°,    По теореме синусов  KL=(LS•sin45°):sin15°  По одной из таблиц значений тригонометрических функций синус 15°=$frac{sqrt{3}-1 }{2sqrt{2} }$ ⇒ KL=(15√2•2√2):2(√3-1)  Произведя сокращения и домножив числитель и знаменатель на (√3+1), получим KL=15•2•(√3-1):(3-1), откуда  KL=15•(√3+1) Площадь ромба равна произведению соседних сторон на синус угла между ними. S=[15(√3+1)]²•√3/2=225•(2√3+3) или 450√3+675 см²