Question

Був дріт з довжиною l . його склали в прямокутник .які його розміри , якщо його площа найбільша ?

Answer 1

Пошаговое объяснение:

Периметр прямоугольника по формуле:

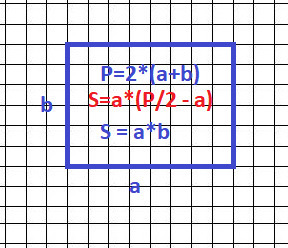
P = 2*(a + b)  - дано.

a + b = P/2 - сумма длин сторон.

Площадь прямоугольника по формуле:

S = a*b = a*(P/2 - a) =  a*P/2  - a² = -(a² - 2*a*P/4 + P²/16) + P²/16.

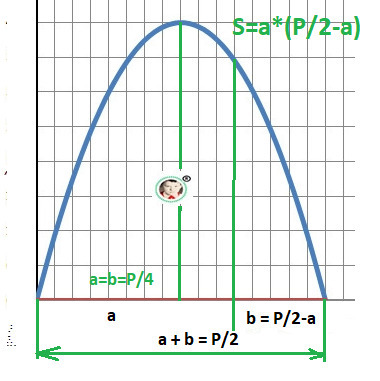
S = - (a - P/4)² + P²/16 - уравнение площади прямоугольника.

Р/4 - значение стороны - а, Smax =Р²/16 - вершина параболы -  максимальное значение.

a  = b =P/4 - сторона квадрата - ответ.

Рисунок к задаче и график площади прямоугольника - в приложении.

Наибольшую площадь при одинаковом периметре имеет квадрат.

Площадь такого квадрата будет:  S = L²/16

Answer 2

"Наибольшую площадь при одинаковом периметре имеет квадрат" - это нужно доказывать.