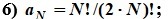Question

Здравствуйте! Помогите срочно составить рекуррентную формулу!

Answer 1

Ответ:

Пошаговое объяснение:

при решении задачи получились 2 формулы

(1) и (2)

по формуле (2) вычислять проще так как при вычислении n не надо отнимать из n+1 единицу а сразу можно использовать n+1

Answer 2

во второй строке из (2n+2) вынесли за скобку 2 и получилось 2(n+1) ; n+1 сократилось с числителем

Answer 3

ччч..., заклинило..., большое спасибо!

Answer 4

Большое вам спасибо! Вы мне очень помогли! Как выяснилось, я делал что-то почти такое же, но в последних вычислениях ошибался, и получал не верный ответ!

Answer 5

Даа, я вон тоже спотыкнулся. Учти только: рекуррентная формула -обязательно 2 штуки (т.е. система) -начальные значения и n-й член (или у меня к-й)

Answer 6

Согласен!

Answer 7

Рекуррентная формула для данной формулы общего члена:
{ а(к)=а(0)=1 при к=0......................(1)
{ а(к)=а(к-1)•1/[2(2к-1)] при к≥1......(2)
где (1) -начальные условия, (2) формула текущего к-го члена через предыдущий (к-1)й член
Проверка: по ф-ле общего члена а(1)=1/2, по рек. ф-ле а(1)=а(0)•1/[2(2*1-1)]=1/2 -совпадает;
по ф-ле о.ч. а(4)=1/1680, а(5)=1/30240, по рек-ной а(5)=(1/1680)•1/[2(2*5)-1)]=1/30240 -совпадает