РЕШИТЕ ПОЖАЛУЙСТА !!!!! с подробным обьяснением очень нужно
Длина стороны ромба АВСД равна 5 см, длина диагонали ВД равна 6 см. Через точку О пересичения диагоналей ромба проведенена
прямая ОК, перпендекулярная его плоскости. Найдите расстояние от точки К до вершин ромба, если ОК = 8 см.
Ответы
Ответ дал:
0
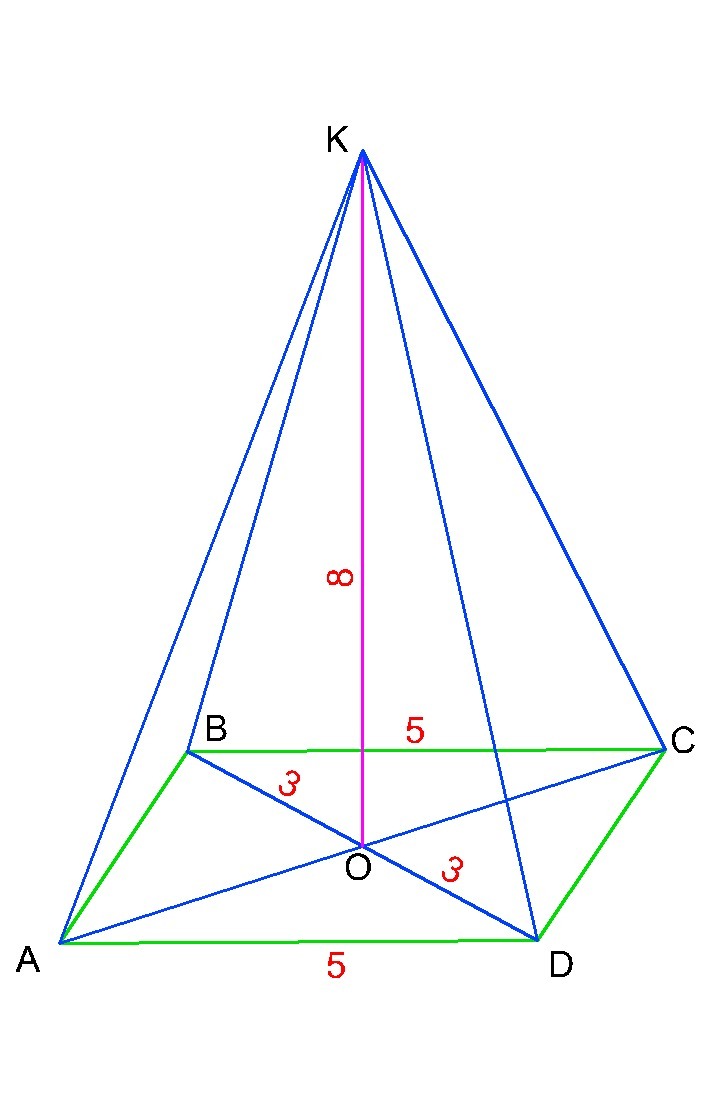
Построим ромб, нормаль ОК, и отрезки КА, КВ, КС, КД.
Рассмотрим прямоугольный ΔКОД. В нем известен катет ОК=8см, катет ОД=ВД/2=3 см (по свойствам диагоналей ромба, точкой пересечения они делятся пополам). Найдем гипотенузу КД=√(64+9)=√73 см.
КД=КВ=√73 см.
Рассмотрим прямоугольный ΔАОД (диагонали ромба пересекаются под прямым углом). В нем известен катет ОД=3 см, гипотенуза АД=5 см. Найдем катет АО=√(25-9)=√16 =4см.
АО в свою очередь является катетом в прямоугольном ΔАОК, где известен второй катет КО=8 см. Найдем гипотенузу КА=√(64+16)=√80
4√5 см.
КА=КС=4√5 см.
Ответ: расстояния от точки К до вершин ромба КД=КВ=√73 см, КА=КС=4√5 см.
Приложения:
Вас заинтересует
2 года назад
2 года назад
3 года назад
3 года назад
9 лет назад
9 лет назад
10 лет назад