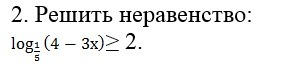Question

Решить неравенство, логарифмы

Answer 1

Ответ:

$frac{33}{25} < x < frac43$

Пошаговое объяснение:

Одз: 4 - 3x > 0, то есть x < 4/3

Теперь возведем 1/5 в соответствующие степени. Так как 1/5 < 1, знак поменяется на противоположный:

$frac{1}{5} ^{log_{frac15}(4-3x) } leq  frac15^2\4 - 3x leq frac{1}{25}\x geq frac{4 - frac{1}{25}}{3}\x geq frac{33}{25}$

Объединяем с Одз и получаем ответ:

$frac{33}{25} < x < frac43$