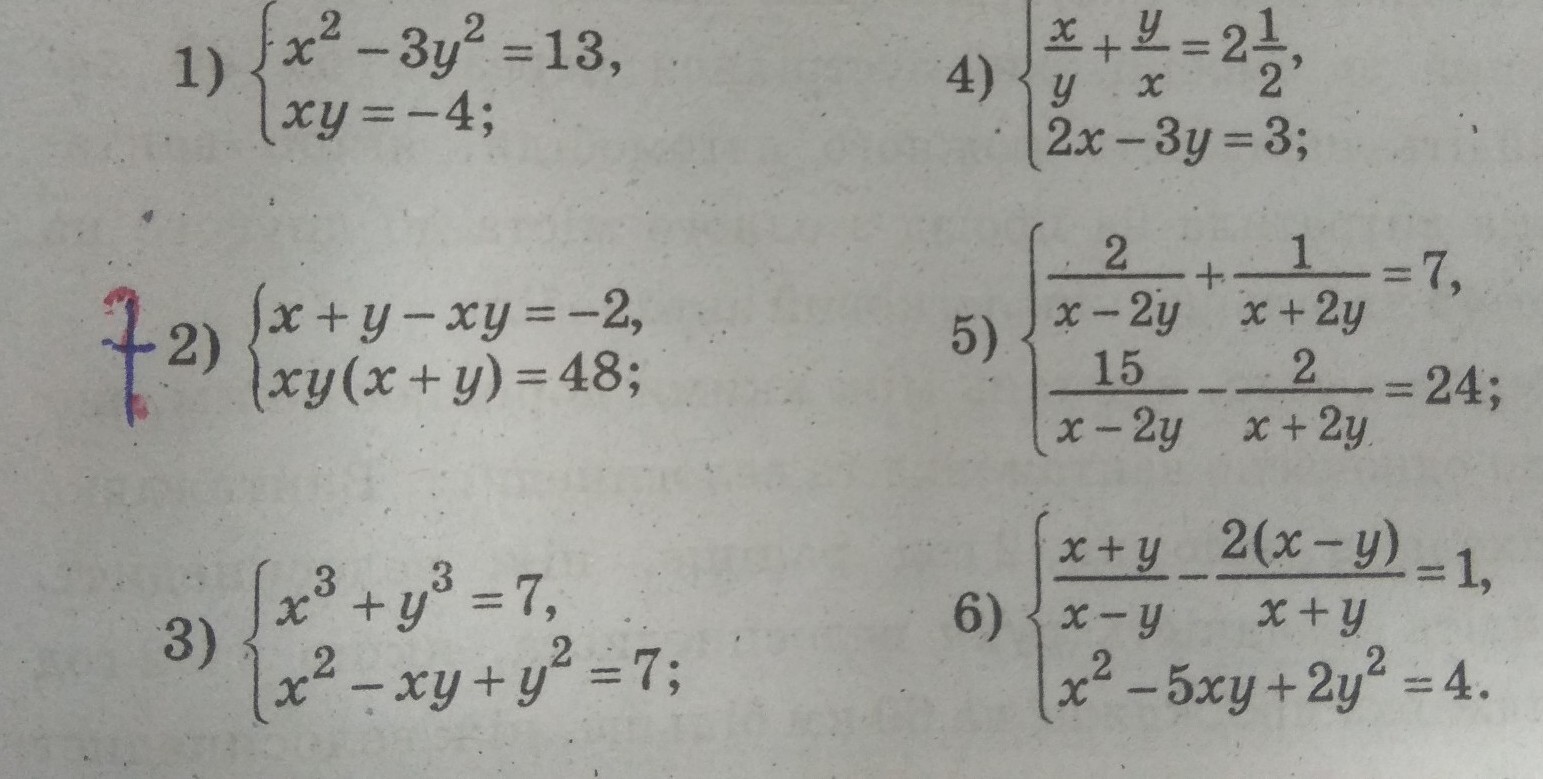Question

Срочно решите пожалуйста 3, 4, 5 и 6!!!! Даю 90 баллов​

Answer 1

3) Ответ: (2; -1), (-1; 2)

$left { {{x^3+y^3=7} atop {x^2-xy+y^2=7}} right. \left { {{(x+y)*(x^2-xy+y^2)=7} atop {x^2-xy+y^2=7}} right. \x+y=1\x=1-y\(1-y)^3+y^3=7\(1-y+y)*((1-2y+y^2)-(1-y)*y+y^2)=7\y^2-2y+1+y^2-y+y^2-7=0\3y^2-3y-6=0\y^2-y-2=0\D=1+4*2=9=3^2\y_1=frac{1-3}{2} =-1;y_2=frac{1+3}{2} =2\x_1=1-(-1)=2; x_2=x-2=-1$

4) Ответ: (-0,75; -1,5), (6; 3)

$2x-3y=3\2x=3y+3\x=1,5y+1,5\x=1,5*(y+1)\\frac{x}{y}+frac{y}{x}=2,5\frac{x^2+y^2}{x*y}=2,5\frac{2,25*(y+1)^2+y^2}{1,5y*(y+1)}=2,5\frac{3,25y^2+4,5y+2,25}{1,5y^2+1,5y}=2,5\3,25y^2+4,5y+2,25=3,75y^2+3,75y\-0,5y^2+0,75y+2,25=0\2y^2-3y-9=0\D=9+4*2*9=81=9^2\y_1=frac{3-9}{2*2}=-1,5; y_2=frac{3+9}{2*2}=3\x_1=1,5*(-0,5)=-0,75; x_2=1,5*4=6$

5) Ответ: ($frac{5}{12};-frac{1}{24}$)

Пусть $frac{1}{x-2y} =a, frac{1}{x+2y} =b$. Тогда система примет вид:

$left { {{2a+b=7} atop {15a-2b=24}} right. \left { {{4a+2b=14} atop {15a-2b=24}} right. \19a=38\a=2\2*2+b=7\b=3$

Вернёмся к нашей замене:

$left { {{x-2y=frac{1}{2} } atop {x+2y=frac{1}{3} }} right. \2x=frac{1}{2}+frac{1}{3}\2x=frac{5}{6} \x=frac{5}{12} \\frac{5}{12}+2y=frac{1}{3}\2y=frac{4}{12} -frac{5}{12} \y=-frac{1}{24}$

6) Ответ: $(0; -sqrt{2}), (0;sqrt{2})$

$frac{x+y}{x-y}-frac{2(x-y)}{x+y}=1\frac{(x+y)^2-2(x-y)^2}{(x-y)(x+y)}=1\x^2+2xy+y^2-2x^2+4xy-y^2=x^2-y^2\6xy-2x^2=0\2x(3y-x)=0\x=0; x=3y\\x=0:\0^2-5*0*y+2y^2=4\y^2=2\x=-sqrt{2}; x=sqrt{2}\\x=3y:\9y^2-15y^2+2y^2=4\-4y^2=4\y^2=-1$

Последнее уравнение не имеет вещественных корней, поэтому берём только случай, когда x=0.

Answer 2

6-е чуть позже скину