Question

найдите расстояние на координатной плоскости между точками А(5;3) и В(2;1)​

Answer 1

См. приложение

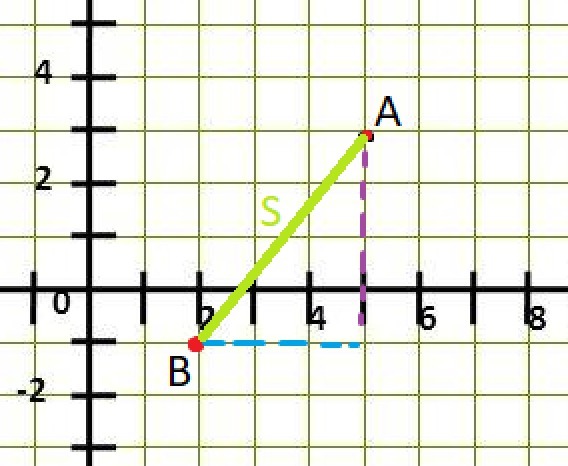
Если представить на координатной плоскости 2 точки, то можно заметить прямоугольный треугольник.

Его катеты - разность соответственных координат А и В

Найдём катеты. Для этого из абсциссы А вычтем абсциссу В

5-2=3 - нижний катет треугольника

Теперь ординаты

3-(-1)=4 -  боковой катет.

По т. Пифагора легко можно найти гипотенузу, а именно она и будет расстоянием между двумя точками

S=$sqrt{3^{2}+4^{2}}=sqrt{25}=5$ - ответ к данной задаче

При чём не важно из какой точки вычитать координаты, потому что под корнем они возводятся в квадрат. Без проблем что что-то получится отрицательное.

Итого, расстояние между двумя точками с координатами (x₁:y₁) и (x₂:y₂)

$S=sqrt{(x_1-x_2)^{2}+ (y_1-y_2)^{2}}$

Answer 2

там B(2;1), а у вас B(2;-1)

Answer 3

в комментариях дали исправление условию