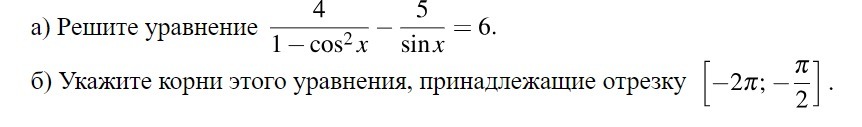Ответы
Ответ дал:
0
В первом случае решений нет
Выбор корней:
оба корня попадают на интервал [-2π;-π/2]
найдем их
Вас заинтересует
2 года назад
2 года назад
3 года назад
3 года назад
9 лет назад
9 лет назад
10 лет назад
10 лет назад