arctg3/7 на промежутке [3Π/2; 5Π/2]
Как найти на числовой окружности
Объясните подробно, пожалуйста
Ответы
Ответ дал:
0
x=arctg3/7
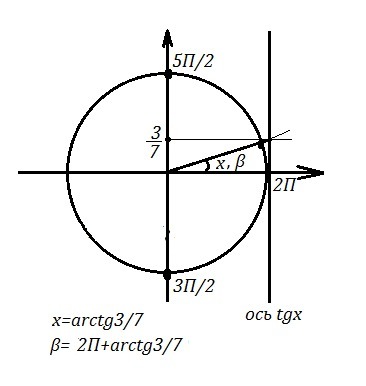
Чтобы построить угол х=arctg3/7 , Надо провести ось тангенсов, она параллельна оси ОУ и проходит через точку с координатами (1,0) . На оси ОУ отложить вверх от начала координат отрезок, равный 3/7, и провести через точку с координатами (0,3/7) прямую, параллельную ОХ. Пересечение полученной прямой и оси тангенсов будет точкой, которую соединим с началом координат. Угол от оси ОХ до последней прямой будет искомым углом х.
Чтобы этот угол принадлежал отрезку [3П/2;5П/2] , надо к 2П прибавить угол х=arctg3/7, получим угол β=(2П+arctg3/7) .
Приложения:
Вас заинтересует
2 года назад
2 года назад
3 года назад
3 года назад
9 лет назад
9 лет назад
9 лет назад