Question

Радиус окружности, вписанной в равносторонний треугольник, равен 5. Найдите высоту этого треугольника.

Answer 1

Давно не решал.

5*3=15

Ответ: 15 Сейчас объясню.

Есть равносторонний треугольник и медиана которая 2:1, считая от вершины, вписанный радиус в его окружность в 3 раза меньше высоты. И искомая высота в 3 раза меньше

Answer 2

И искомая высота в 3 раза больше радиуса* Ошибка

Answer 3

Ответ:   15

Объяснение:

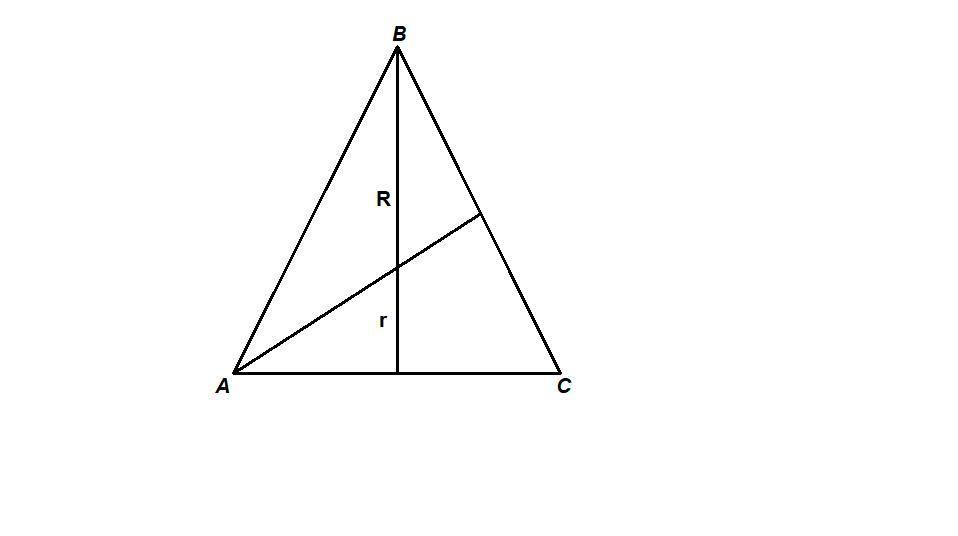
Для равностороннего треугольника центры вписанной и описанной окружности совпадают и лежат в точке пересечения медиан (биссектрис, высот).

Точка пересечения медиан делит их в отношении 2 : 1, считая от вершины, поэтому медиана ВН, она же и высота, в 3 раза больше радиуса вписанной окружности:

ВН == 3r = 3 · 5 = 15.