Ответы
Ответ дал:
0
решение задания смотри на фотографии
Приложения:
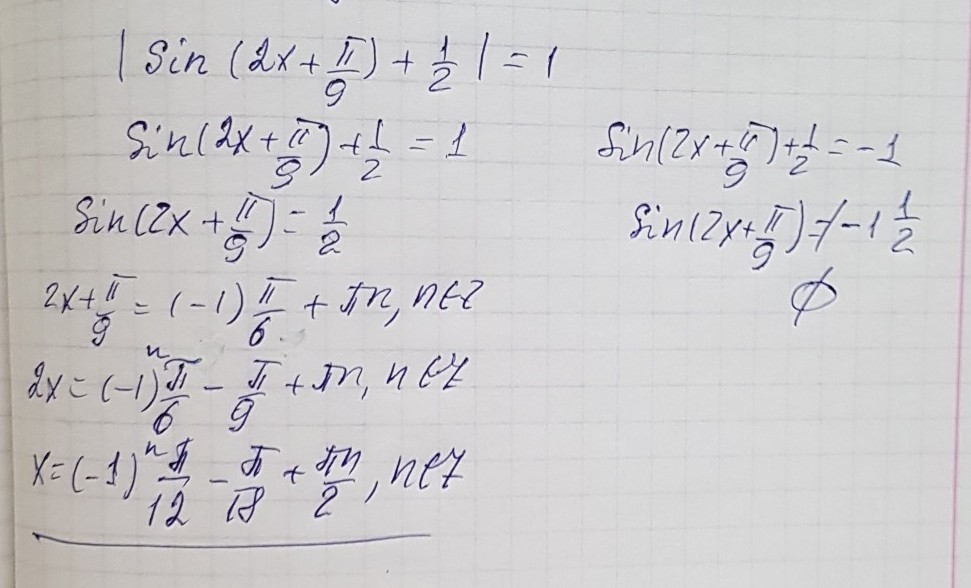
Ответ дал:
0
По определению модуля:
sin(2x+(π/9)) +(1/2)= -1 или sin(2x+(π/9))+(1/2) = 1
sin(2x+(π/9)) +(1/2)= -1 ⇒ sin(2x+(π/9)) = -3/2
уравнение не имеет корней по свойству ограниченности синуса
-1 ≤ sin(2x+(π/9)) ≤1
sin(2x+(π/9)) = 1/2 ⇒2x+(π/9)=(-1)^(k)(π/6)+πk, k∈Z
Удобнее записать в виде двух серий ответов при k=2n и k=2m+1:
2x+(π/9)=(π/6)+2πn, n∈Z или 2x+(π/9)=(-π/6)+2πm+π, m∈Z
2x=(-π/9)+(π/6)+2πn, n∈Z или 2x= (-π/9)+(5π/6)+2πm, m∈Z
2x=(π/18)+2πn, n∈Z или 2x= (13π/18)+2πm, m∈Z
x=(π/36)+πn, n∈Z или x= (13π/36)+πm, m∈Z
О т в е т. (π/36)+πn, n∈Z; (13π/36)+πm, m∈Z
Приложения:
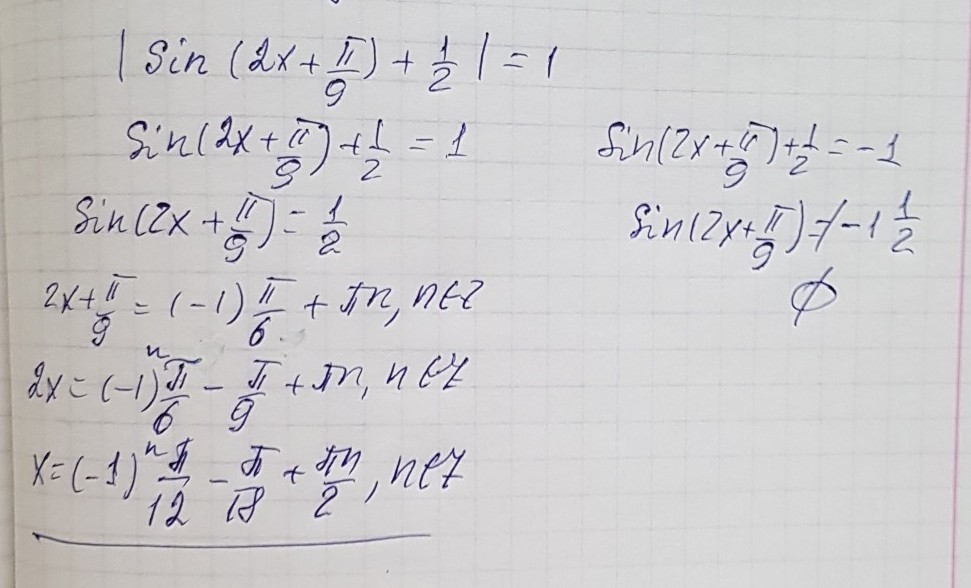
Вас заинтересует
2 года назад
3 года назад
9 лет назад
10 лет назад
10 лет назад