Question

Решите показательное неравенство (Подробно)
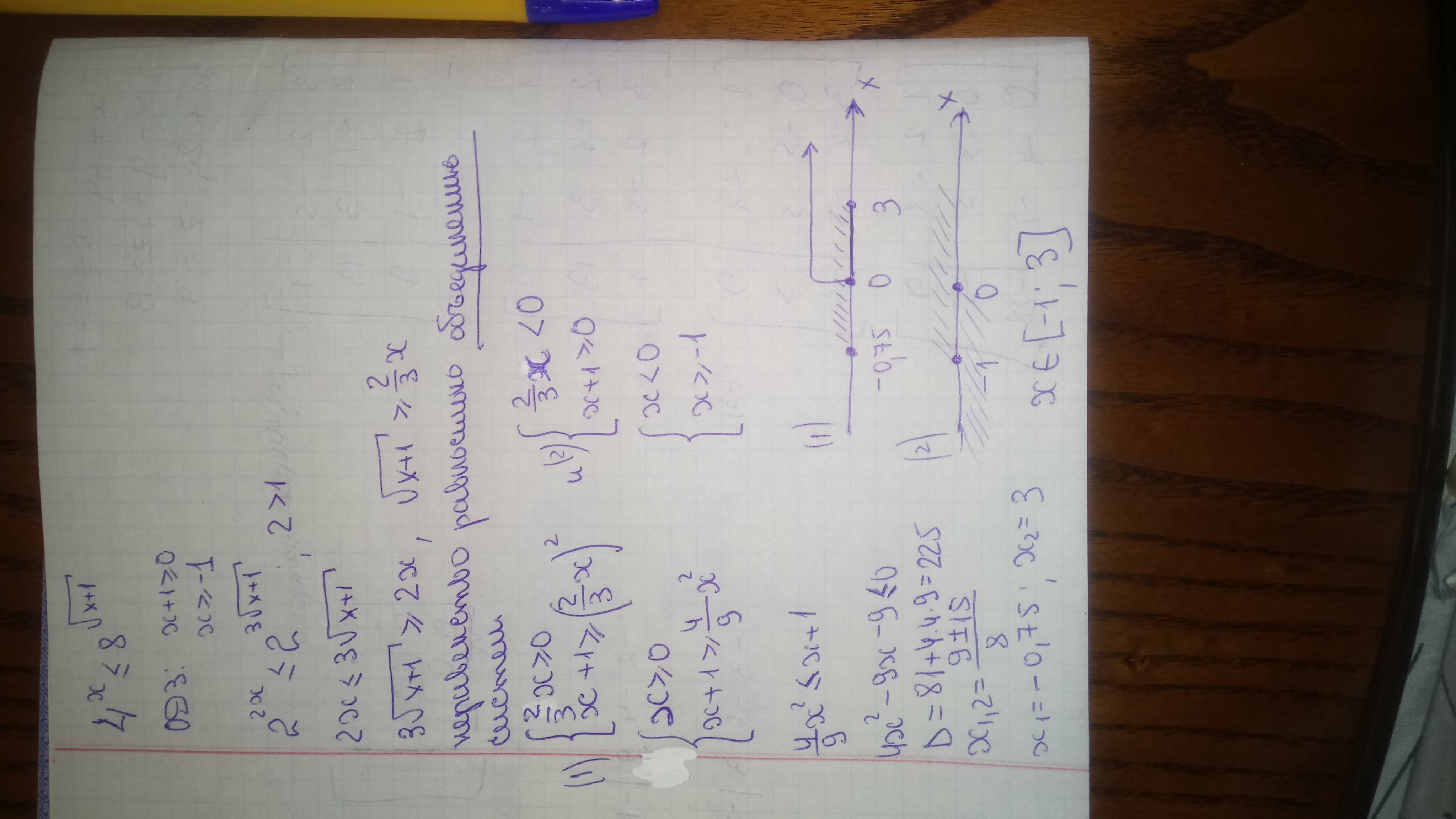
4.6 1) 4^x<=8^sqrt(x+1) Ответ: [-1;3]
6.8 sqrt(2^x-3)>=3-2^0.5x Ответ: [2; + бесконечность)

Желательно в письменном виде...
Cм.фотографию
Ответы были найдены с помощью калькулятора

Answer 1

Решение задания приложено 4. 6

Answer 2

А 6.8 уже не хочу решать. Кто-то не дал шанс добавить, спешит вперёд паровоза. А после отметки нарушения это не возможно сделать

Answer 3

Модератору привет.

Answer 4

А , это умник WhatYouNeed поставил нарушение. Ну-ну...

Answer 5

У Вас очень хорошие решения))

Answer 6

Я отметил нарушение, не полное решение, что верно. Зачем добавлять решение, а потом редактировать и добавлять ещё одно, надо сразу всё, не всегда можно редактировать.
И что вам не нравится в моём решении?

Answer 7

4.6

$2^{2x}leq 2^{3sqrt{x+1} }\3sqrt{x+1} geq 2x\left[begin{array}{ccc}left { {{2x/3<0} atop {x+1geq 0}} right. \left { {{2x/3geq 0} atop {x+1geq 4x^2/9}} right. \end{array}$

$left[begin{array}{ccc}left { {{x<0} atop {xgeq -1}} right. \left { {{xgeq 0} atop { 4x^2-9x-9leq 0}} right. \end{array}$

D=9*9+16*9=225

$(x-(9-15)/8)(x-(9+15)/8)leq 0$

$left[begin{array}{ccc}left { {{x<0} atop {xgeq -1}} right. \left { {{xgeq 0} atop {(x+0,75)(x-3)leq 0}} right. \end{array}$

Ответ: x∈[-1;3]

6.8

$sqrt{2^x-3} geq 3-2^{0.5x}\2^x=a\sqrt{a-3}geq 3-sqrt{a} \left[begin{array}{ccc}left { {{3-sqrt{a}<0} atop {a-3geq 0}} right. \left { {{3-sqrt{a}geq 0} atop {a-3geq 9+a-6sqrt{a} }} right. \end{array}$

$left[begin{array}{ccc}left { {{sqrt{a}>3} atop {ageq 3}} right. \left { {sqrt{a}leq 3} atop {sqrt{a} geq 2}} right. \end{array}$

$left[begin{array}{ccc}left { {{a>9} atop {ageq 3}} right. \left { {0leq aleq 9} atop {a geq 4}} right. \end{array}$

$left { {{2^x>9} atop {4leq 2^xleq 9}} right. \left { {{x>log2(9)} atop {log2(4)leq xleq log2(9)}} right. \2leq x$

Ответ: [2;+∞)

Answer 8

Хм, у тебя ошибка в первом

Answer 9

возможно опечатка