Question

Найти возрастание и убывание производных f(x)= все под корнем 4x-x^2

Answer 1

$f(x)=sqrt{4x-x^2}\f'(x)=frac{(4x-x^2)'}{2sqrt{4x-x^2}}=\frac{4-2x*1}{2sqrt{4x-x^2}}=frac{-(x-2)}{sqrt{4x-x^2}};\4x-x^2>0; x^2-4x<0=>0<x<4\f''(x)=(frac{-x+2)}{sqrt{4x-x^2}})'=frac{-1*sqrt{4x-x^2}-frac{(-x+2)*(4x-x^2)'}{2sqrt{4x-x^2}}}{sqrt{4x-x^2}^2}=frac{frac{(x-2)(4-2x)}{2sqrt{4x-x^2}}-sqrt{4x-x^2}}{4x-x^2}=\frac{frac{-(x-2)(x-2)-4x+x^2}{sqrt{4x-x^2}}}{4x-x^2}=frac{-x^2+4x-4-4x+x^2}{sqrt{4x-x^2}*(4x-x^2)}=frac{-4}{-x(x-4)sqrt{4x-x^2}}$

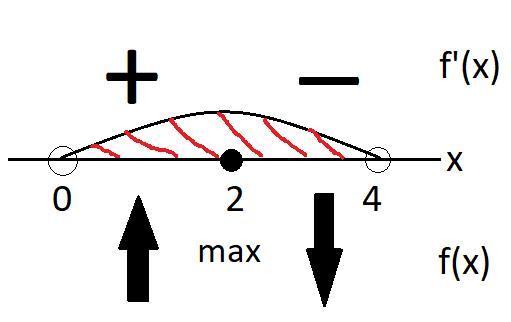
Когда производная положительная - функция возрастает, а производная убывает (т.к. через вторую производную мы нашли, что кривая всегда выпуклая и первая производная равна тангенсу угла касательной к точке функции), когда отрицательная производная - функция убывает, а производная уменьшается (всегда выпуклая кривая).

Ответ: функция : возрастает - (0;2); убывает - (2;4)

            производная убывает - (0;4)