Question

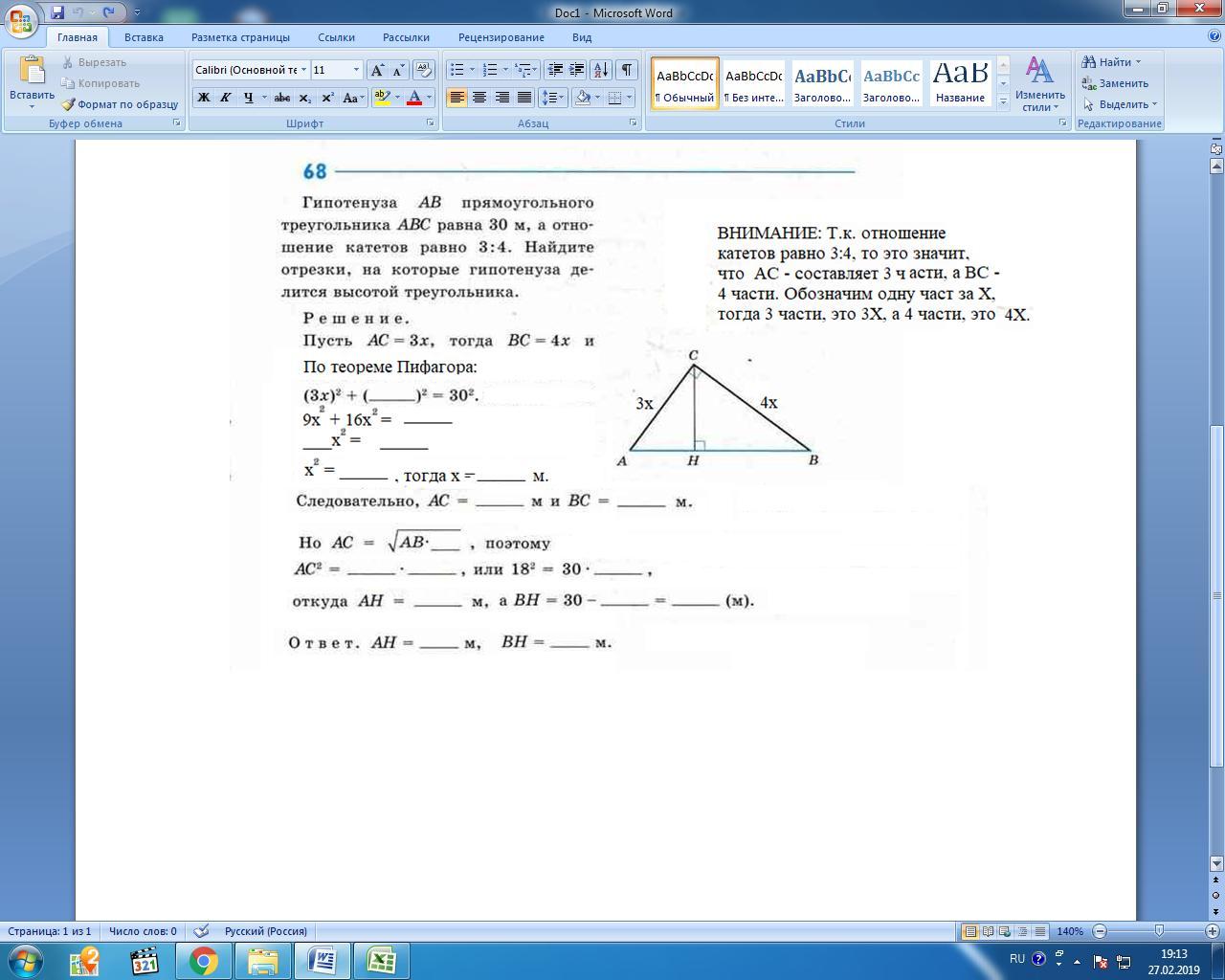
Гипотенуза AB прямоугольного треугольника ABC равна 30 м, а отношение катетов равно 3:4. Найдите отрезки, на которые гипотенуза делится высотой треугольника.

Answer 1

Решение

Пусть AC=3x , тогда BC=4x (3x)^2+(4x)^2=30^2 . Отсюда 25x^2=900 , x^2=36 и x=6 . Следовательно , AC=18 м и BC=24 м  . Но AC=корень AB*AH , по-этому AC^2=AB*AH , или 18^2=30*AH , отсюда AH=10,8 , а BH=30-10,8=19,2 м

Ответ AH=10,8 м

          BH=19,2 м