Ответы
Ответ дал:
0
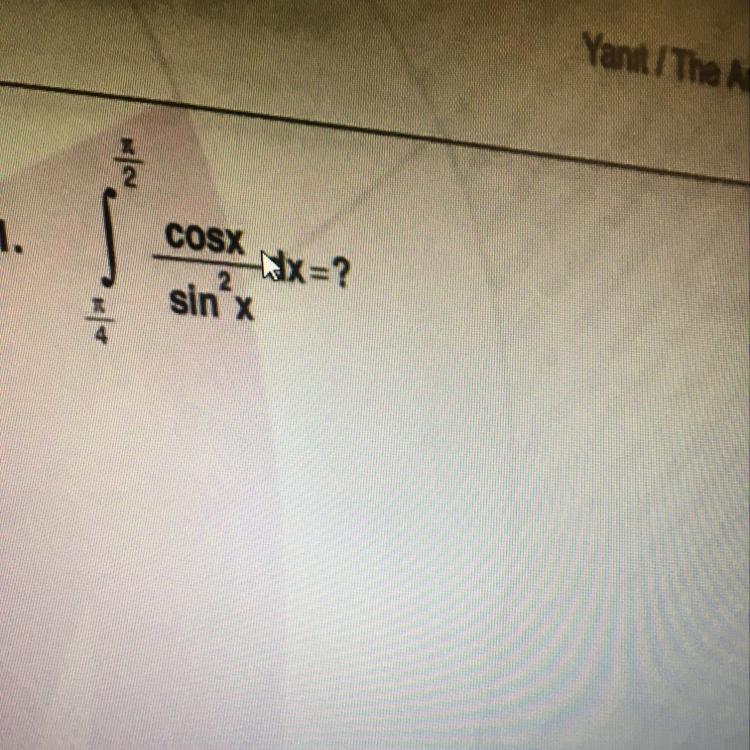
Чтобы вычислить такой интеграл, надо хорошо знать производные элементарных функций. Для этого примера надо помнить, что .
Вас заинтересует
2 года назад
2 года назад
3 года назад
3 года назад
9 лет назад
10 лет назад