Ответы
Ответ дал:
0
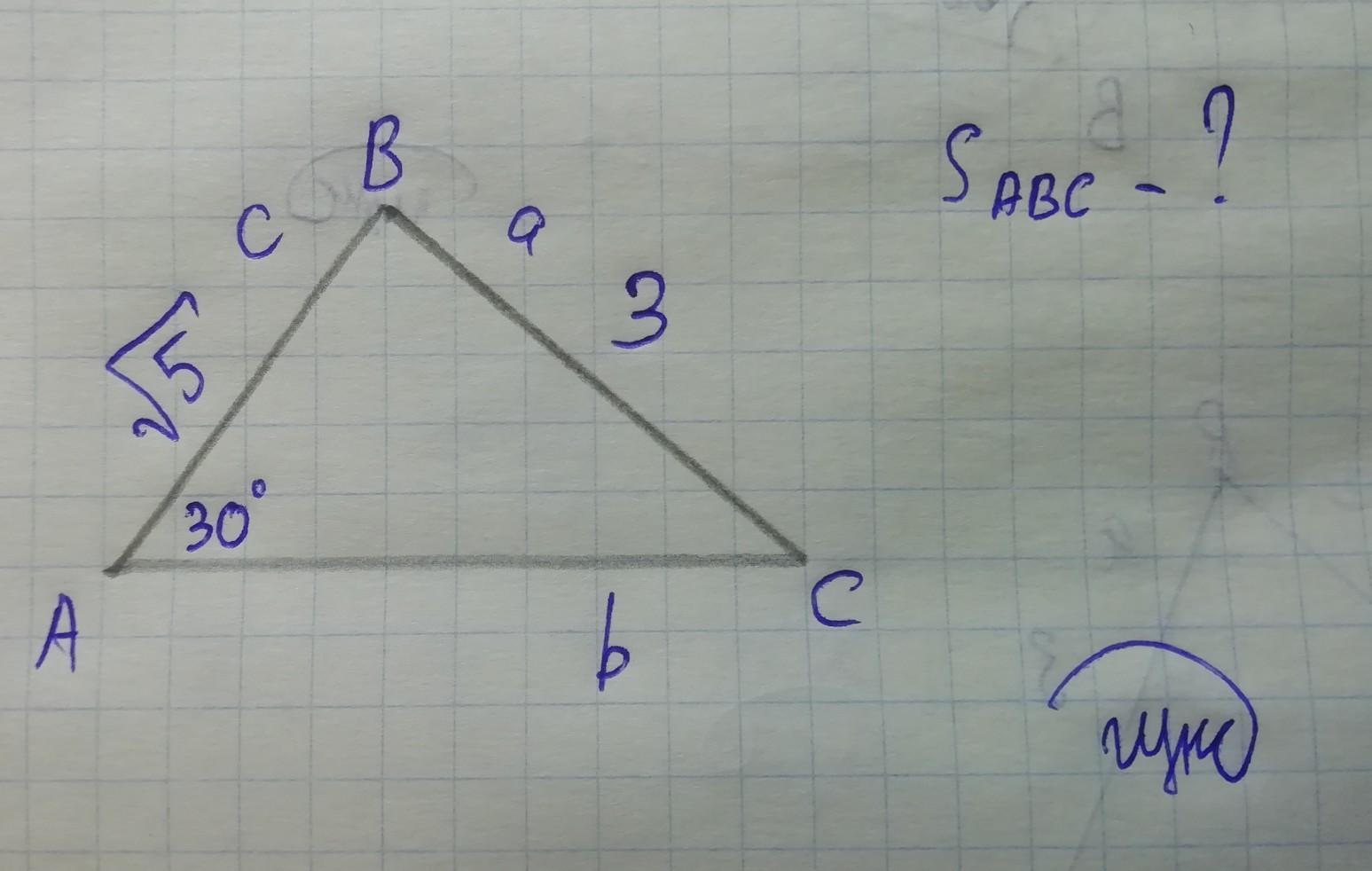
По теореме синусов найдем синус ∠C и вычислим его значение

Синус в 0,37 есть угол в ≈22° ==> ∠C ≈ 22°
∠B = 180 - ∠A - ∠C = 180 - 30 - 22 ≈ 128°
Площадь треугольника равна половине произведения двух его сторон на синус угла между ними


Ответ: S(ABC) ≈ 2,6 см²
Синус в 0,37 есть угол в ≈22° ==> ∠C ≈ 22°
∠B = 180 - ∠A - ∠C = 180 - 30 - 22 ≈ 128°
Площадь треугольника равна половине произведения двух его сторон на синус угла между ними
Ответ: S(ABC) ≈ 2,6 см²
Приложения:
Вас заинтересует
2 года назад
2 года назад
3 года назад
3 года назад
9 лет назад
9 лет назад
10 лет назад
10 лет назад