Question

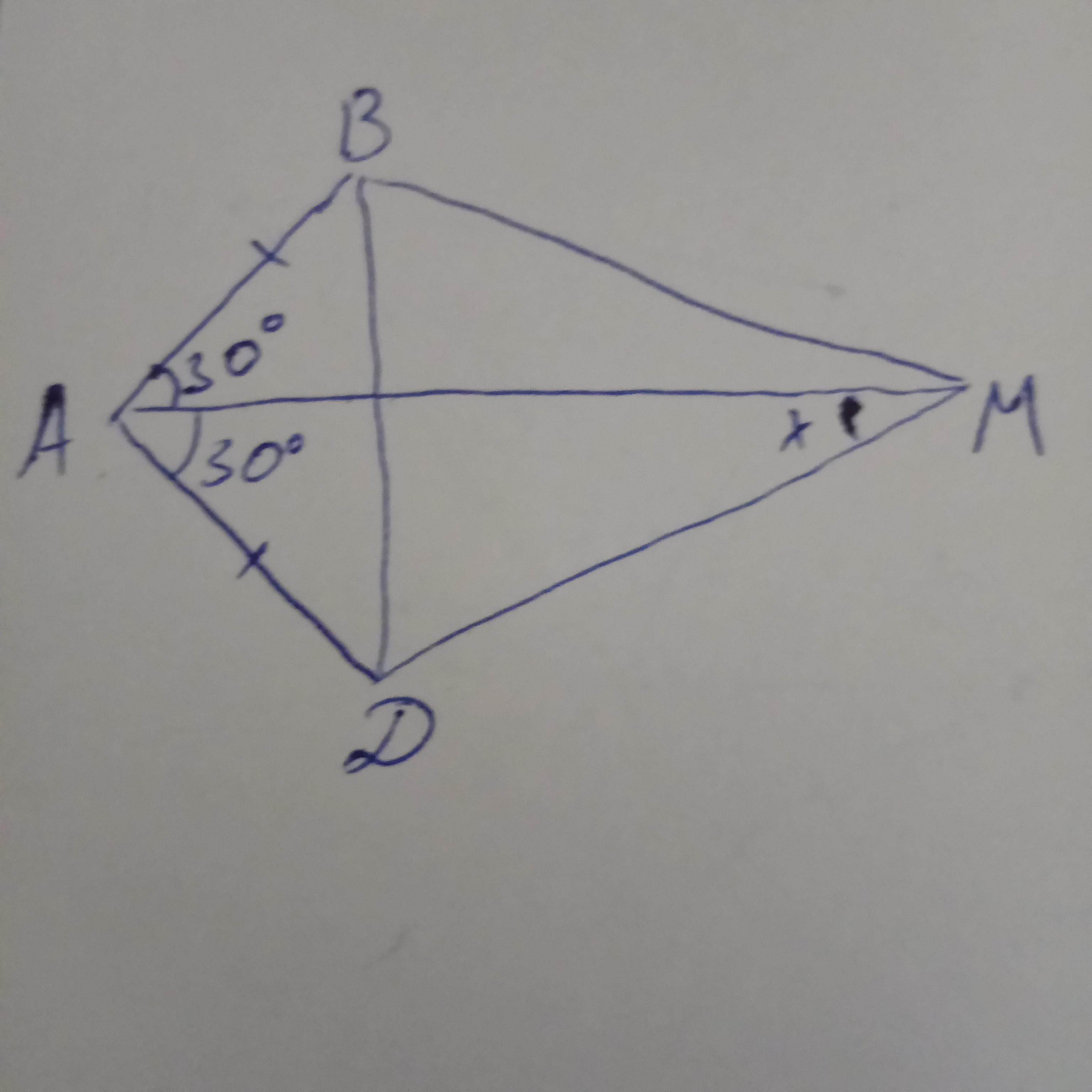
Дан выпуклый четырёхугольник ABMC,в котором AB=BC угол BAM равен 30 градусам,угол ACM равен 150 градусам. Докажите,что AM - биссектриса угла BMC.

Answer 1

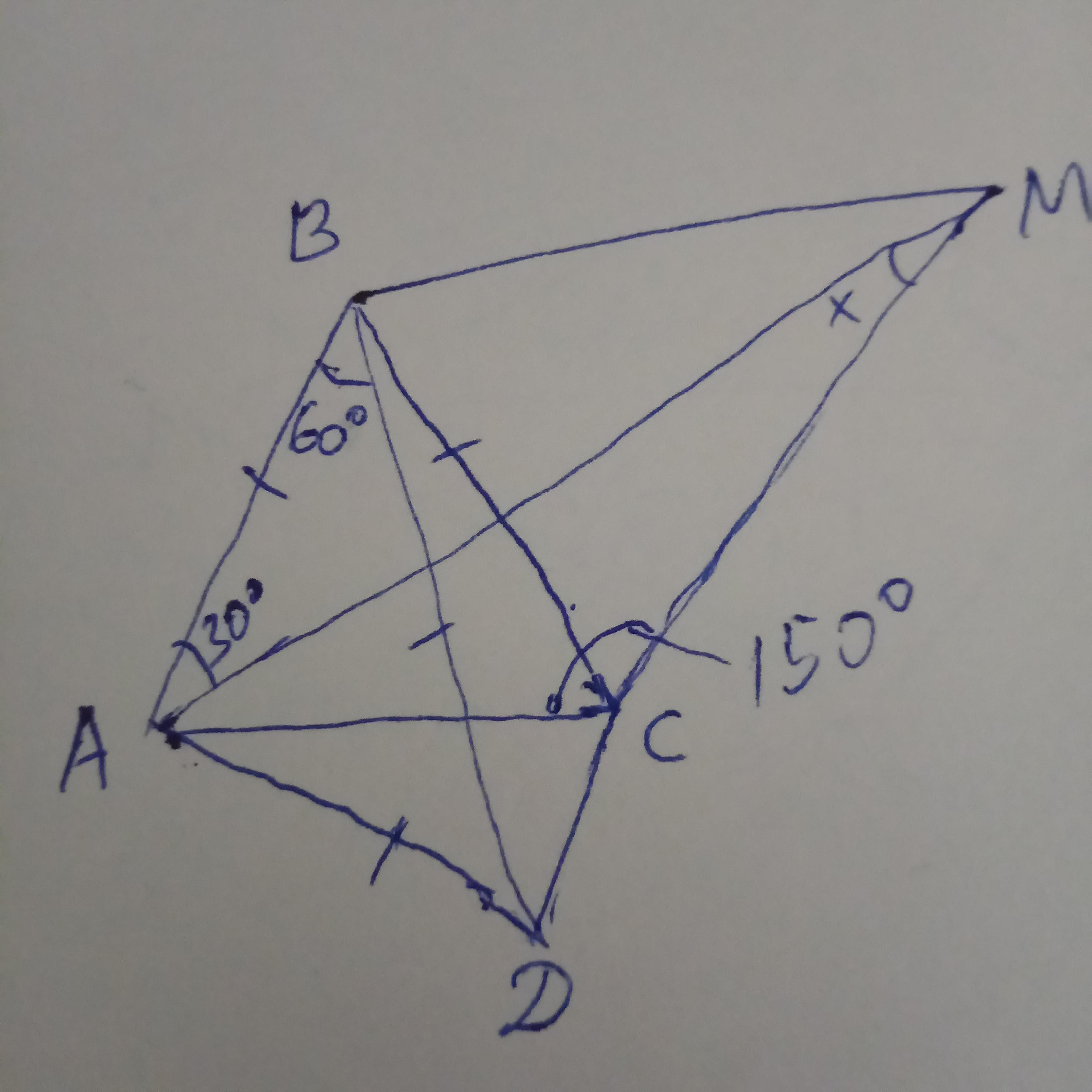
Проведём от точки А отрезок AD, таким образом, чтобы угол BAD был равен 60° и АВ был равен AD. Получаем равносторонний треугольник АВD.

Обозначим угол AMD как x, тогда угол МАС=180-150-х=30-х.

угол ВАС=BCA=30+30-х=60-х

угол АВС=180-2*(60-х)=60+2х

угол СВD=60+2x-60=2x

угол BCD=BDC=(180-2x)/2=90-x

Угол АСD=90-x-(60-x)=30°

угол DCM=150+30=180°

Т.к. угол DCM - развернутый, то будем рассматривать четырехугольник АВМD, а именно треугольники АВМ и АDM. Они равны, т.к. угол BAM=DAM, AB=AD и сторона АМ - общая. Следовательно угол BMA=DBA.

Это значит, что АМ - биссектриса угла BMD.

Answer 2

Странно, что я не один, кто решает так громоздко))) Киньте ссылку на второе решение в личку)

Answer 3

если хотите я его ненадолго покажу здесь-потом удалю

Answer 4

второе окно ответа пока недоступно

Answer 5

скопируйте его да удалю я его

Answer 6

удаляю?