Question

Сторона квадрата равна α. Найти площадь закрашенной области.

Answer 1

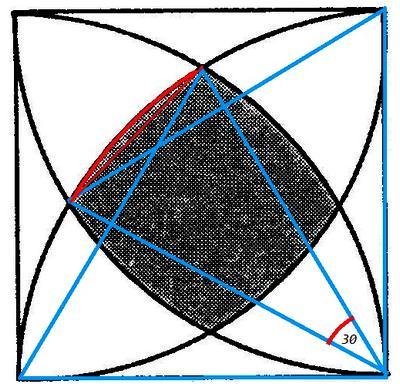
Разделим искомую фигуру на квадрат со стороной x и четыре сегмента окружности, радиус a, угол 30.  

По теореме косинусов  

x^2= 2a^2 -2a^2 cos30 = a^2(2-√3)  

Площадь сегмента, радиус a, угол 30

Sсег= пa^2 30/360 -a^2 sin30/2 = a^2(п/12 -1/4)  

S= x^2 +4Sсег = a^2(2-√3) +a^2(п/3 -1) = a^2(1 +п/3 -√3)

Answer 2

Есть задача о трисекции прямого угла.

Answer 3

трисекция-это что?

Answer 4

если только из-за меня-то менять ничего не надо....

Answer 5

i.imgur.com/ic5iGyP.png

Answer 6

спасибо, я разберусь попозже)