Дана линейная неоднородная система уравнений. Исследовать систему на совместность тремя способами и решить ее :
1) по формулам Крамера
2) матричным методом
3) методом Гаусса
а) 3х1-х2+4х3-10=0 б) 2х1+х2-х3=5
2х1+3х2-х3-3=0 х1-2х2+2х3=-5
х1-4х2+2х2-1=0 7х1+х2-х3=10
Ответы
Ответ дал:
0
Очень старался не ошибиться в подсчётах. Обратную в первом случае искал трижды и три раза получал разные результаты, так что просто посчитал правильный ответ в MatLab и вписал в решение.
КАК использовать обратную для нахождения неизвестных я указал. А обратную можно найти или через или методом приведения к канонической форме
или методом приведения к канонической форме  . Чаще использую второй метод так, как подсчёт
. Чаще использую второй метод так, как подсчёт  занимает больше времени, но в данном случае - фиаско в арифметике :)
занимает больше времени, но в данном случае - фиаско в арифметике :)
В третим в очереди идёт метод Крамера, который в первом варианте вернул вектор, а во втором указал на "бесконечное" множество решений (если мы над |R - тогда бесконечное как есть).
Этот-же вывод получаем из равенства 3-rankA=1 => существует нетривиальный ответ в гомогенной системе (A|0), что указывает на "бесконечность" решений.
Вроде всё. Возникнут вопросы - пиши!
КАК использовать обратную для нахождения неизвестных я указал. А обратную можно найти или через
В третим в очереди идёт метод Крамера, который в первом варианте вернул вектор, а во втором указал на "бесконечное" множество решений (если мы над |R - тогда бесконечное как есть).
Этот-же вывод получаем из равенства 3-rankA=1 => существует нетривиальный ответ в гомогенной системе (A|0), что указывает на "бесконечность" решений.
Вроде всё. Возникнут вопросы - пиши!
Приложения:
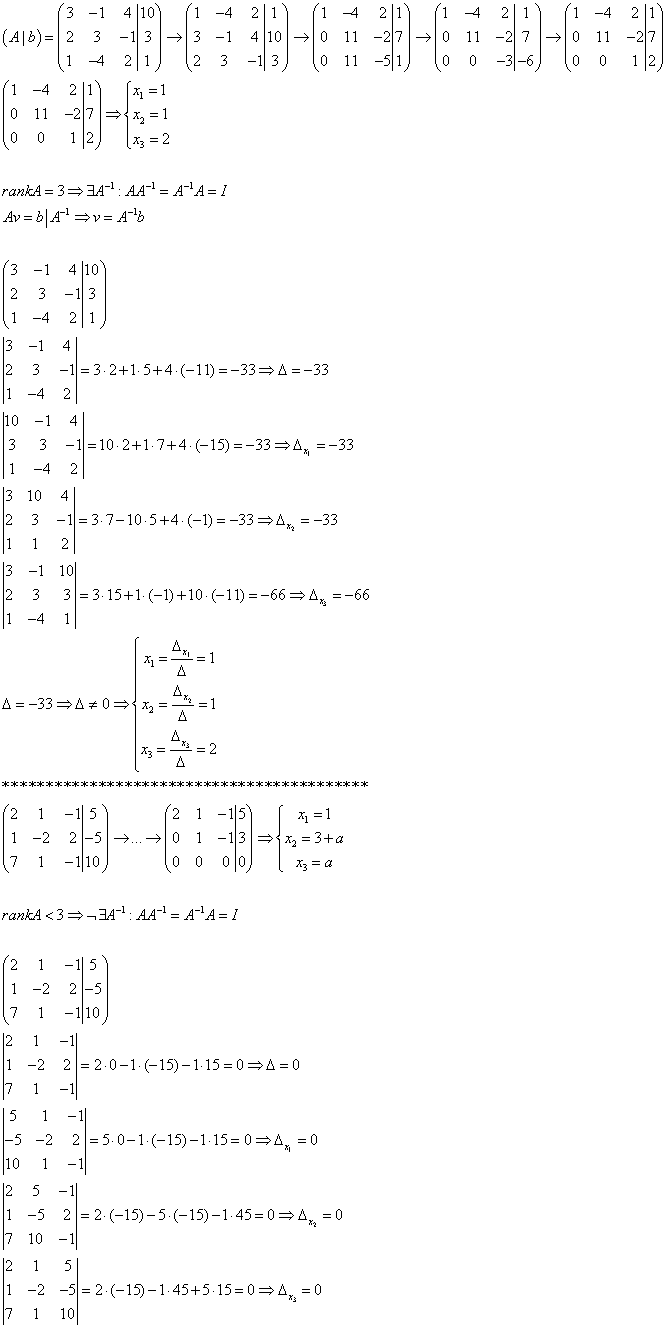
Вас заинтересует
2 года назад
2 года назад
8 лет назад
8 лет назад
10 лет назад
10 лет назад
10 лет назад