Question

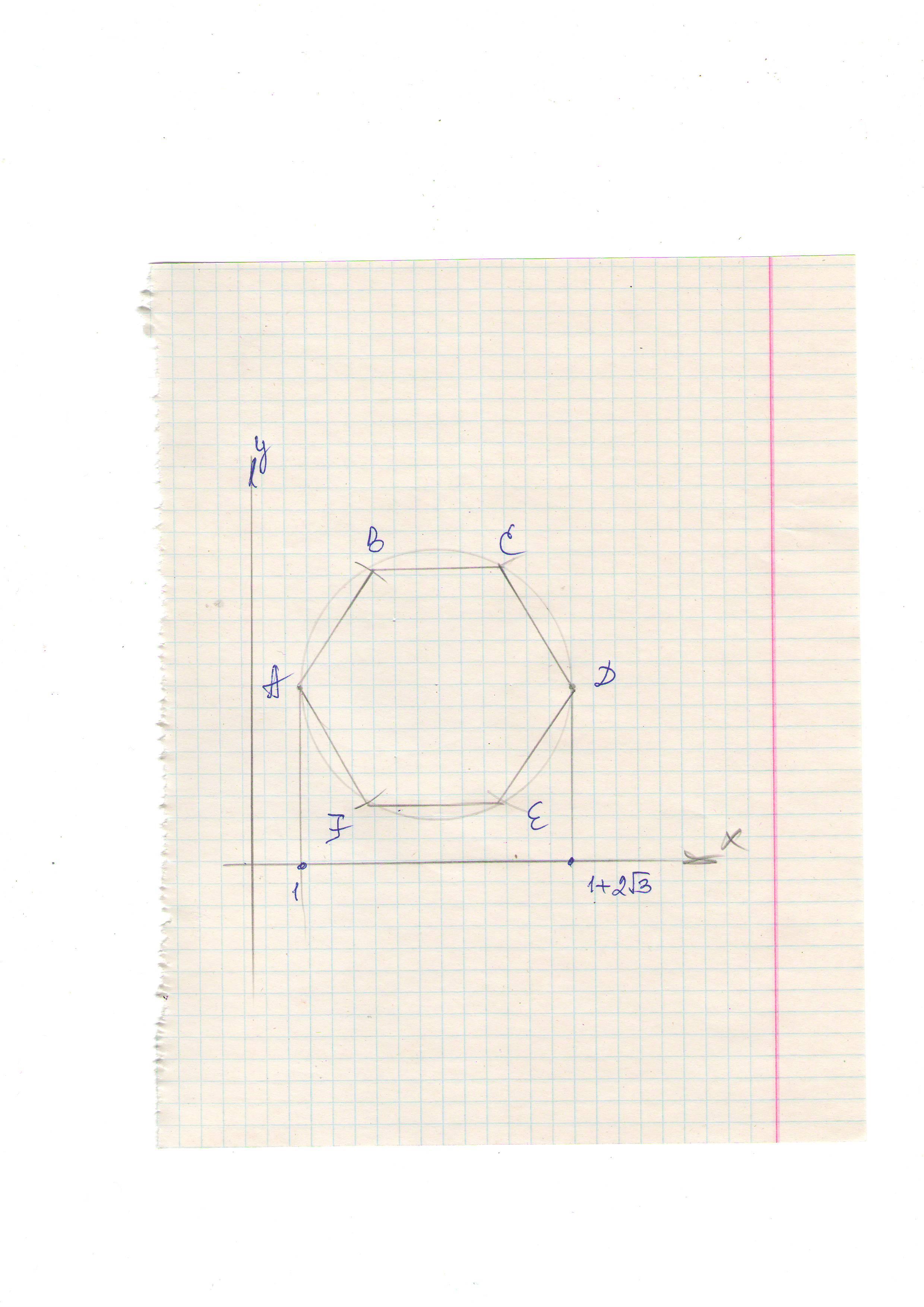
Найдите радиус окружности, вписанной в правильный
шестиугольник ABCDEF, если абсцисса точки А равна 1, абсцисса точки D равна
1 + 2√3, ординаты точек А и D равны.

Answer 1

AD - это диаметр окружности. AD = 1 +2√3 -1 = 2√3

радиус будет в 2 раза меньше.

Ответ: R = √3

Answer 2

подождите, AD не может быть диаметром вписанной окружности

Answer 3

Ну, ё-моё! Точно. Я не увидел

Answer 4

Надо вписанную окружность!

Answer 5

Надо СЕ искать. Это диаметр вписанной окружности. т. Пифагора. СЕ/2 = 1,5 Сори.

Answer 6

Ничего , случается )

Answer 7

на фото.................

Answer 8

помоги еще с задачей пожалуйста
https://znanija.com/task/32336099