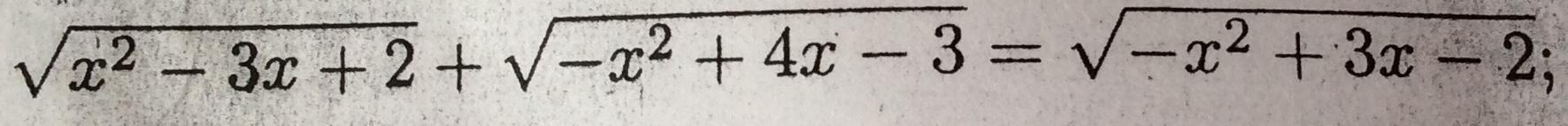Question

Помогите решить уравнение. Вроде бы решил, но сомневаюсь в решении.

Answer 1

$sf sqrt{x^2-3x+2}+sqrt{-x^2+4x-3}=sqrt{-x^2+3x-2}$

Запишем и решим ОДЗ уравнения.

$left { begin{array}{I} sf x^2-3x+2geq0 \ sf -x^2+4x-3geq0 \ sf -x^2+3x-2geq0 end{array} Rightarrow left { begin{array}{I} sf (x-1)(x-2)geq0 \ sf (x-1)(x-3)leq0 \ sf (x-1)(x-2)leq0 end{array} Rightarrow left { begin{array}{I} sf xin(-infty; 1] cup [2; +infty) \ sf x in [1; 3] \ sf xin [1; 2] end{array}$

Заметим, что в ОДЗ входят лишь две отдельно стоящие точки - x=1 и x=2. Проверим, является ли хотя бы одна из них корнем уравнения.

$sf boxed{sf x=1} Rightarrow sqrt{1-3+2}+sqrt{-1+4-3}=sqrt{-1+3-2} Rightarrow 0+0=0 checkmark \ sf boxed{sf x=2} Rightarrow sqrt{4-6+2}+sqrt{-4+8-3}=sqrt{-4+6-2} Rightarrow 0+1=0 times$

Ответ: x=1

Answer 2

Так в любом случае x=1 или x=2 кандидаты. Нужно просто подставить и посмотреть

Answer 3

При других x будет корень из отрицательного выражения

Answer 4

Это по сути и есть учет одз

Answer 5

да оно понятно, но мало ли. Хуже от этого точно не будет

Answer 6

Ну ок

Answer 7

Заметим что:

x^2-3x+2= -(-x^2+3x-2)

Тк корень из отрицательного числа невозможен,то подкоренное выражение может быть равно только нулю

x^2-3x+2=0

x1=1

x2=2

Подставим оба корня в уравнение:

Если  x=2  получаем:

1=0  (невозможно)

при  x=1   решение подходит

Ответ: x=1

Answer 8

x=1

Answer 9

опечатка

Answer 10

Перезагрузи

Answer 11

Решение изменено