Докажите, что отрезок, соединяющий середины основания трапеции, делит трапецию на две равновеликие трапеции!
Приложения:
Ответы
Ответ дал:
0
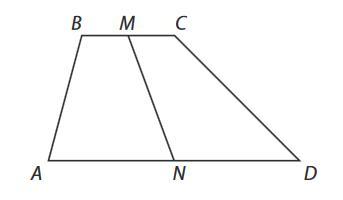
Пусть АN=ND=a; BM=MC=b; MN=h- высота трапеции. Тогда площадь каждой из частей, на которые отрезок MN делит трапецию равна S=h*((a+b):2), то есть эти части равновелики
Ответ дал:
0
Ответ:
Пошаговое объяснение:
Так как у трап. АBMN и MNCD высоты одинаковые , а так же точка М и N делит ВС и АD на 2 равные отрезки соответственно ⇒ по формуле нахождения площади Sabmn = Smncd
Вас заинтересует
2 года назад
2 года назад
3 года назад
9 лет назад
10 лет назад
10 лет назад