Question

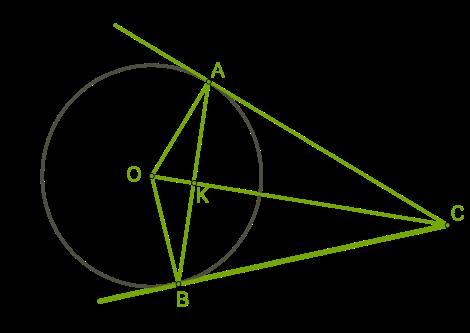
Из точки C проведены две касательные к окружности, точки касания — A и B . Определи равные отрезки и углы.

1.AO=

2.AC=

3.∡BCO =

4. ∡BOC =

5. ∡OBC =

Answer 1

Ответ:

AO=1,5см

AC=4см

BCO=45 градусов

BOC=60 градусов

OBC=90 градусов

Answer 2

Ответ:

1. АО = ВО как радиусы.

2. АС = ВС как отрезки касательных, проведенных из одной точки.

3. ∠ВСО = ∠АСО, так как центр окружности, вписанной в угол, лежит на биссектрисе этого угла.

4. ∠ВОС = ∠АОС.

Равенство этих углов следует из равенства треугольников ВОС и АОС:

ОА = ОВ как радиусы,

∠ОАС = ∠ОВС = 90°, так как радиус, проведенный в точку касания, перпендикулярен касательной,

ОС - общая сторона,  ⇒

ΔВОС = ΔАОС по катету и гипотенузе.

5. ∠ОВС = ∠ОАС = 90°, так как радиус, проведенный в точку касания, перпендикулярен касательной.