Ответы
Ответ дал:
0
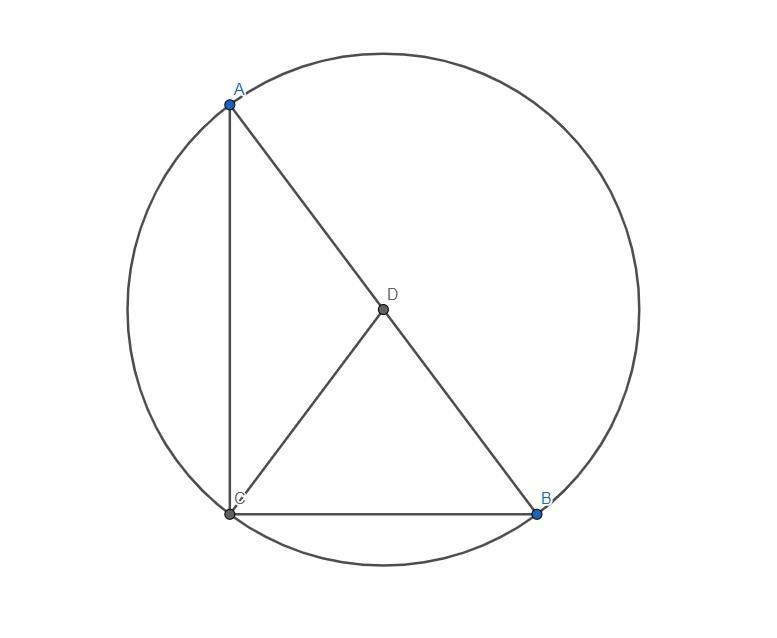
В прямоугольном треугольнике ABC проведем медиану CD. Построим окружность с центром в точке D и радиусом, равным AD.
Точка B также будет лежать на данной окружности, т.к медиана CD разделила отрезок AB на стороны AD=DB, следовательно AB - диаметр
По условию угол ACB - прямой и опирается на диаметр AB, следовательно угол ACB - вписанный, поэтому точка С также лежит на окружности, значит CD - радиус и будет равен AD и DB по определению радиуса.
AD и AB - половины гипотенузы. Таким образом, медиана, проведенная к гипотенузе равна половине гипотенузы, что и требовалось доказать.
Приложения:
Вас заинтересует
2 года назад
3 года назад
9 лет назад
9 лет назад
10 лет назад
10 лет назад

