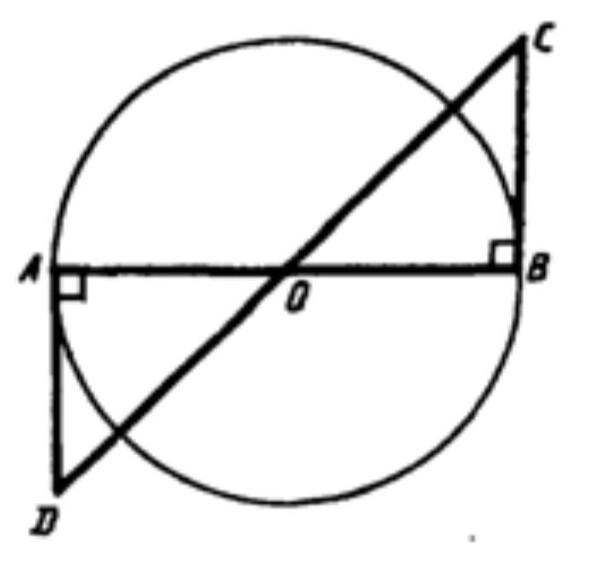
О — центр
окружности. Через концы
отрезка АВ проведены пря-
мые AD и ВС, перпендику-
лярные к прямой АВ. Дока-
жите, что ADO = OCB.
Приложения:
Ответы
Ответ дал:
0
Ответ:
Пошаговое объяснение:
∠AOD≈∠COB так как они вертикальные
∠OAD≈∠CBO так как оба 90°
AO≈OB так как оба радиусы⇒
⇒ΔAOD≅ΔCOB по УСУ (угол сторона угол)
Ответ дал:
0
Решение:
1) ∠OAD=∠OBC (прямые)
2) ∠COB=∠DOA (как вертикальные)
3) АО=ОВ (радиусы)
Отсюда треугольники ADO и ОСВ равны по второму признаку равенства треугольников.
(Также, если необходимо, исходя из равенства треугольников углы ADO и OCB будут равны)
Вас заинтересует
2 года назад
3 года назад
3 года назад
10 лет назад