Question

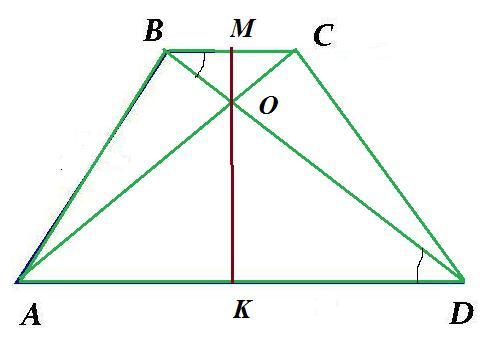
В трапеции ABCD известны длины оснований AD=25 , BC=15. Диагонали AC и BD пересекаются в точке O. Найдите площадь трапеции ABCD, если площадь треугольника AOD равна 125

Answer 1

S(ΔAOD)=(1/2)AD·OK

Δ AOD ~ ΔBOC по двум углам

∠СAD=∠BCA- внутренние накрест лежащие

∠AOD=∠BOC -как вертикальные.

пусть ОК - высота Δ AOD; OM - высота Δ ВОС

Так как из точки О можно провести только один перпендикуляр к прямой, а значит и к параллельной ей прямой

KM⊥BC  и KM ⊥ AD

Из подобия

AD:BC=OK:OM

OK:OM=25:15=5:3

OK=5k; OM=3k

k- коэффициент пропорциональности.

S( Δ AOD)=(1/2)AD·OK

(1/2)AD·OK=125

OK=250/AD=250/25=10

5k=10

k=2

OM=3k=3·2=6

KM=16

S ( трапеции)=(AD+BC)·KM/2=(25+15)·16/2=320