Диагональ равнобокой трапеции перпендикулярна боковой стороне, а угол между диагональю и высотой трапеции равен альфа. Найдите радиус окружности, описанной около трапеции, если ее высота равна h.
Ответы
Ответ дал:
0
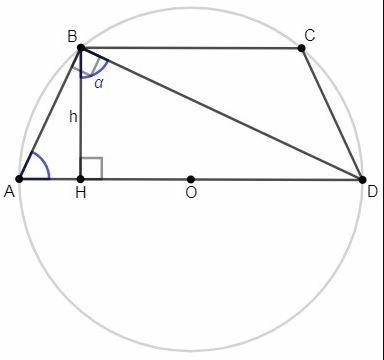
∠ABD=90°, ∠BHD=90°, ∠DBH =a, BH=h
∠A= 90°-∠BDA =∠DBH =a
△BHD:
tg(a)= HD/BH <=> HD=h*tg(a)
△AHB:
ctg(a)= AH/BH <=> AH=h*ctg(a)
AD =AH+HD =h(tg(a)+ctg(a))
Трапеция ABCD - равнобедренная, следовательно ее можно вписать в окружность. Угол ABD - прямой, следовательно опирается на диаметр окружности (AD), описанной около треугольника ABD и трапеции ABCD.
R= AD/2 =(tg(a)+ctg(a))h/2
Приложения:
Вас заинтересует
2 года назад
2 года назад
3 года назад
3 года назад
9 лет назад
9 лет назад
9 лет назад