Question

Алгебра. Тригонометрия. Даю 98 баллов!

Answer 1

$displaystyle sin^22x+sin^24x=1-frac{cos2x}{cos3x}\\ODZ: cos3xneq 0; xneq frac{pi }{6}+frac{pi n}{3}\\frac{1-cos4x}{2}+frac{1-cos8x}{2}=1-frac{cos2x}{cos3x}\\frac{2-(cos4x+cos8x)}{2}=1-frac{cos2x}{cos3x}\\1-frac{cos4x+cos8x}{2}=1-frac{cos2x}{cos3x}\\frac{cos4x+cos8x}{2}=frac{cos2x}{cos3x}$

$displaystyle frac{2cos6x*cos2x}{2}=frac{cos2x}{cos3x}\\cos6x*cos2x*cos3x=cos2x\\cos2x(cos6x*cos3x-1)=0$

1)

$displaystyle cos2x=0; 2x=frac{pi }{2}+pi n; x=frac{pi }{4}+frac{pi n}{2}; nin Z$

2)

$displaystyle cos6x*cos3x-1=0\\(2cos^23x-1)*cos3x-1=0\\ 2cos^33x-cos3x-1=0\\ (cos3x-1)(2cos^23x+2cos3x+1)=0\\cos3x=1; 3x=2pi n; x=frac{2pi n}{3}; nin Z\\2cos^23x+2cos3x+1=0$

решений нет

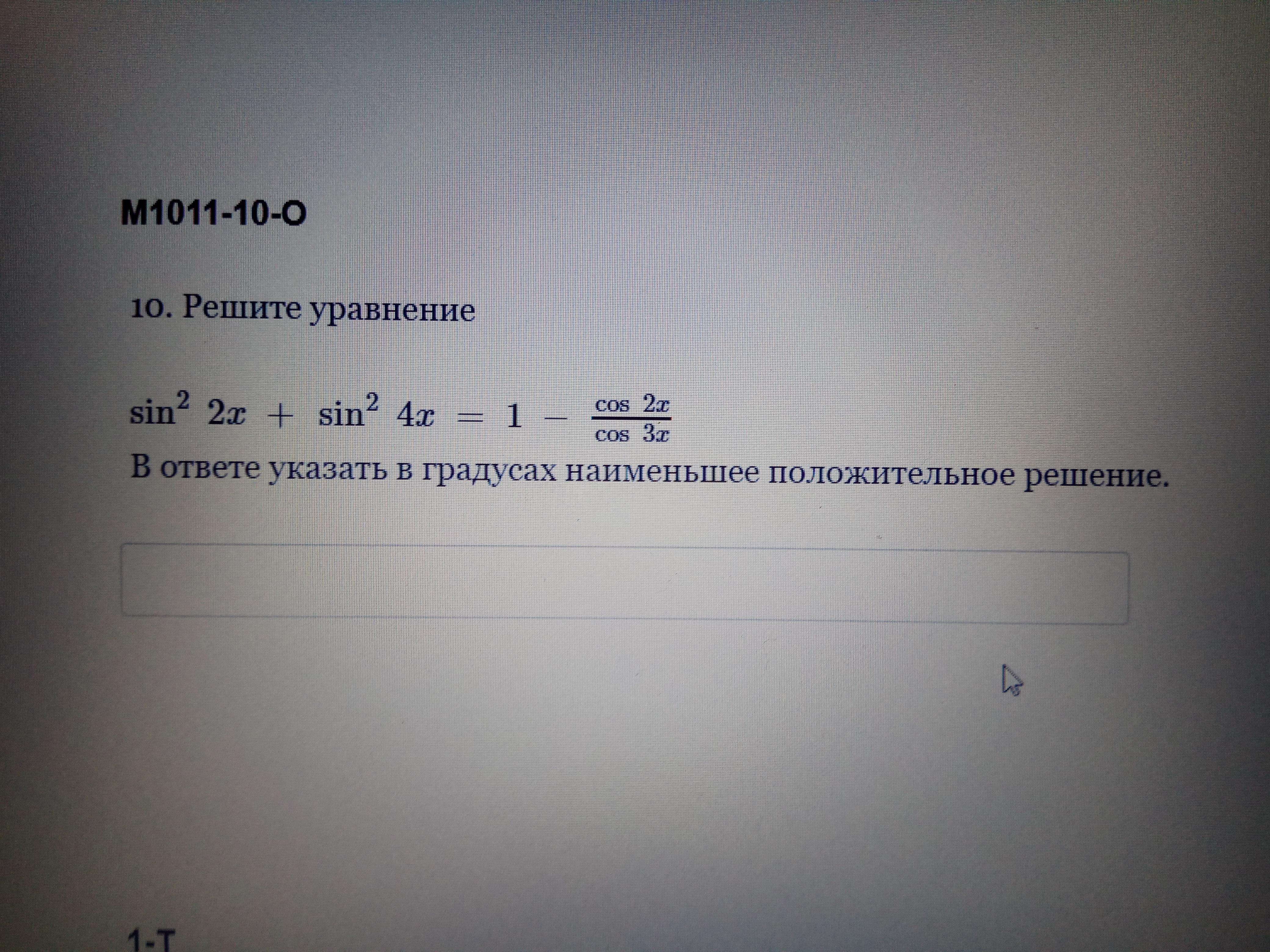
общее решение х=π/4+πn/2; n∈Z

                            x= 2πn/3; n∈Z

Наименьшее положительное решение х=π/4

p.s. Решение кубического уравнения с помощью схемы Горнера

Answer 2

по второй строке 2) "2" не потеряно?

Answer 3

подкорректировала запись

Answer 4

Спасибо, проверил. Решал правильно значит)

Answer 5

Только намного проще