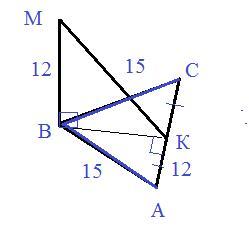
Дан равносторонний треугольник ABC, где AB=CB=15 см, AC=24 см. Из высоты B к плоскости треугольника проеден перпендикуляр BM. Определить расстояние от пункта М до стороны треугольника АС, если известно, что BM=12 см
Ответы
Ответ дал:
0
ВМ⊥ пл. АВС⇒ВМ⊥АС⇒Δ ВMК - прямоугольный.
Проводим ВК⊥АС
ВК - проекция MK
По теореме о трех перпендикулярах
наклонная MK⊥AC
Длина МК и есть расстояние от М до АС
ΔАВС- равнобедренный, значит ВК и высота и медиана,
АК=КС=12
Из прямоугольного треугольника АВК по теореме Пифагора
ВК²=АВ²-АК²=15²-12²=81
ВК=9
Из прямоугольного треугольника ВMК по теореме Пифагора
MК²=ВM²+BК²=12²+9²=144+81=225
MK=15 см
Приложения:
Вас заинтересует
2 года назад
2 года назад
3 года назад
3 года назад
9 лет назад
9 лет назад
9 лет назад
9 лет назад