ССССССРРРРРОООООЧЧЧЧННННОООО!!!
алгебра 8 класс!
Докажите, что при любом а верно неравенство
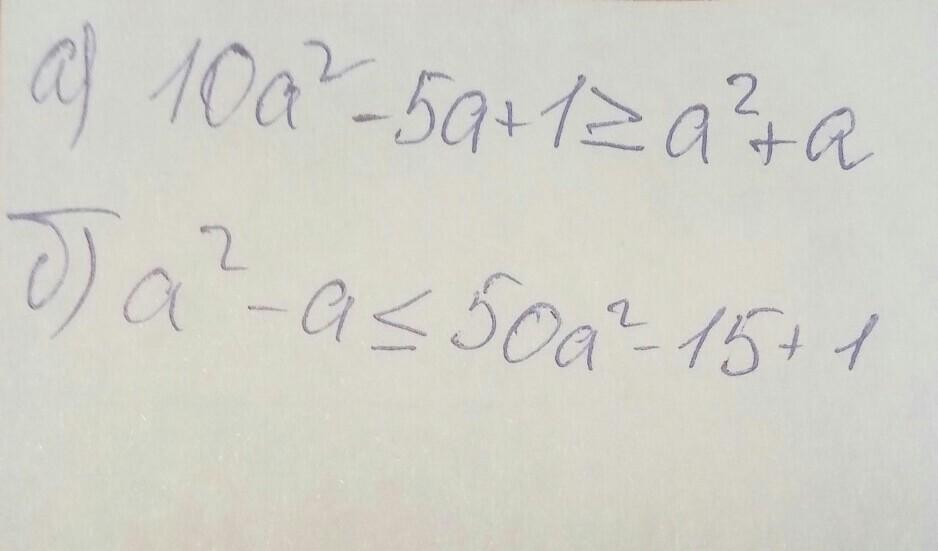
Ответы
10а²-5а+1≥а²+а
9а²-6а+1≥0
(3а-1)²≥0 четная степень всегда ≥0
а²-а≤50а²-15+1
49а²-14а+1≥0
(7а-1)²≥0
Ответ:
a) Доказано
б) Доказано
Пошаговое объяснение:
Ответ:
Пошаговое объяснение:
a)
Из обеих частей вычитаем правую часть.
Получаем:
9a^2-6a+1>=0
Преобразуем в квадрат разности:
(3a-1)^2>=0
Квадрат любого числа больше или равен нулю.
При a = 1/3 соблюдается условие о равенстве, при любом другом значении аргумента, выражение будет положительным.
б)
По всей видимости, в записи допущена ошибка: справа не 15, а 15a
Из обеих частей вычитаем левую часть.
Получаем:
49a^2-14a+1>=0
Преобразуем в квадрат разности:
(7a-1)^2>=0
Квадрат любого числа больше или равен нулю.
При a = 1/7 соблюдается условие о равенстве, при любом другом значении аргумента выражение будет положительным.