Ответы
Ответ дал:
0
Ответ: x={ 4π/3+2πn; 5π/3+2πn}, n∈Z.
Приложения:
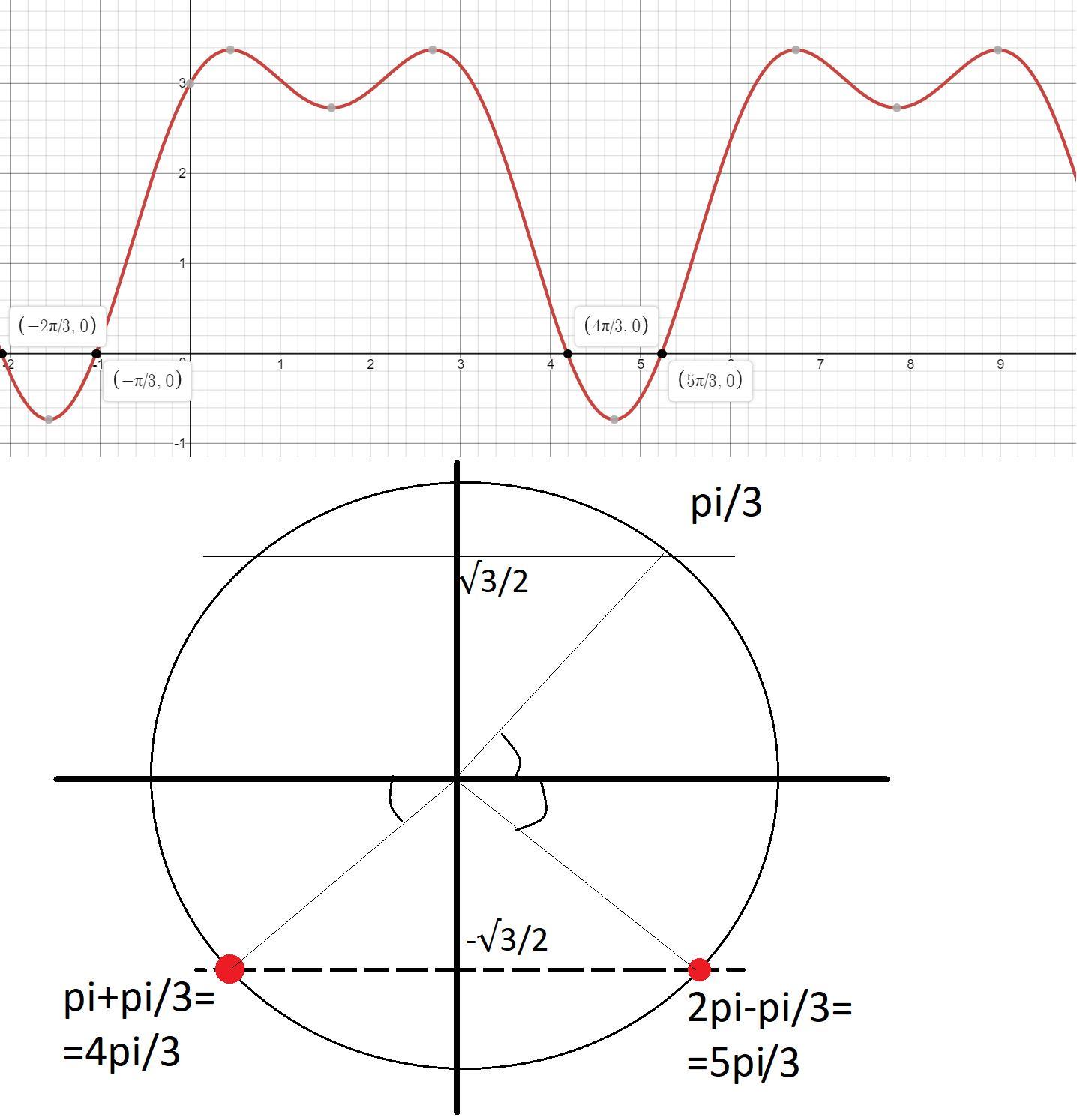
Ответ дал:
0
а почему два ответа ведь корень из 3 sin не существует
Ответ дал:
0
Да согласен, я сделал переход и наисал что только -корень из 3 разделить на 2. Посмотри на тригонометрический круг, там всё видно. Сейчас к ответу добавлю файлы
Вас заинтересует
2 года назад
2 года назад
3 года назад
3 года назад
9 лет назад