Question

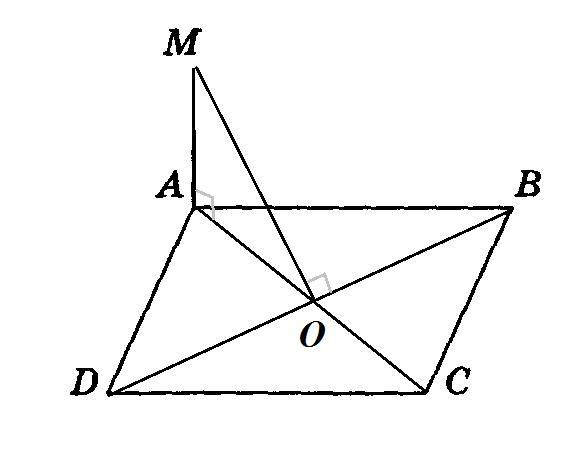
Ma-перпендикуляр до площини паралелограма аbcd, о - середина bd і mo перпендикулярні bd. 1) визначте вид паралелограма abcd. 2) знайдіть відстань від точки m до площини паралелограма якщо кут abc=60° ad=24cм ma=13см.

Answer 1

MO⊥BD

По теореме о трёх перпендикулярах

АО⊥ BD ⇒ диагонали  параллелограмма взаимно перпендикулярны, знначит АВСD - ромб.

∠АВС=60° ⇒Δ АВС - равносторонний

АС=АВ=ВС=AD=24 cм

АО=(1/2)АС=12 см

По теореме Пифагора из прямоугольного треугольника МАО ( MA⊥ пл. АВСD, значит и прямой АО)

Дано МО=13

Найти МА

МA²=MO²-AO²=13²-12²=169-144=25

MA=5