Question

Помогите привести уравнение кривой второго порядка к каноническому виду, выяснить, что это за кривая. Найти координаты смещенного центра. Построить кривую на плоскости

3x^2+2y^2+2*3x+2*20y-45=0

Answer 1

Дано уравнение кривой 3x²+2y²+2*3x+2*20y-45=0.

Выделим полные квадраты: 3(x²+2x+1)-3+2(y²+20y+100)-200-45=0.

Получаем 3(х+ 1)² + 2(у + 10)² = 248.  Разделим обе части на 248.

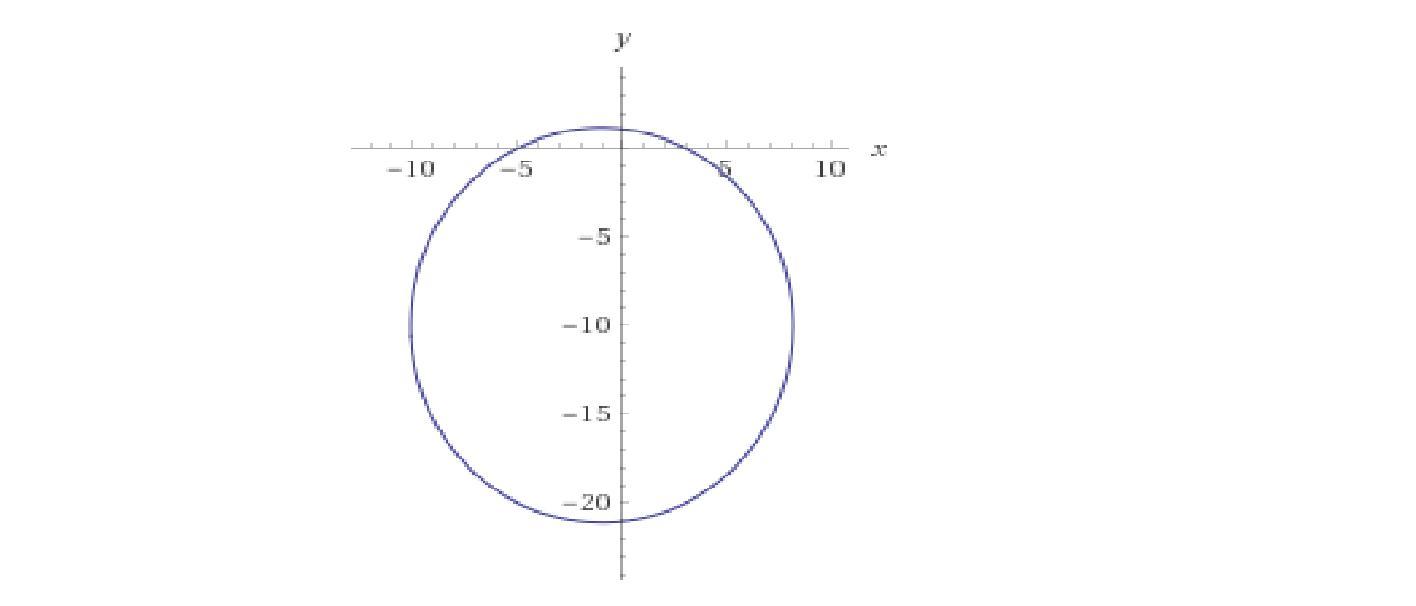
((х+ 1)²/(248/3)) + ((у + 10)²)/124 = 1.  Это уравнение эллипса.

Его центр (-1; -10).

Малая ось равна √(248/3) ≈ 9,09212 параллельна оси Ох.

Большая ось равна √124 ≈ 11,13553  параллельна оси Оу.