Ответы
Ответ дал:
0
1. Область определения:
x∈(-∞;-1)∪(-1;2)∪(2;+∞)
2. Функция общего вида.
3. Найдём точки пересечения с осями:
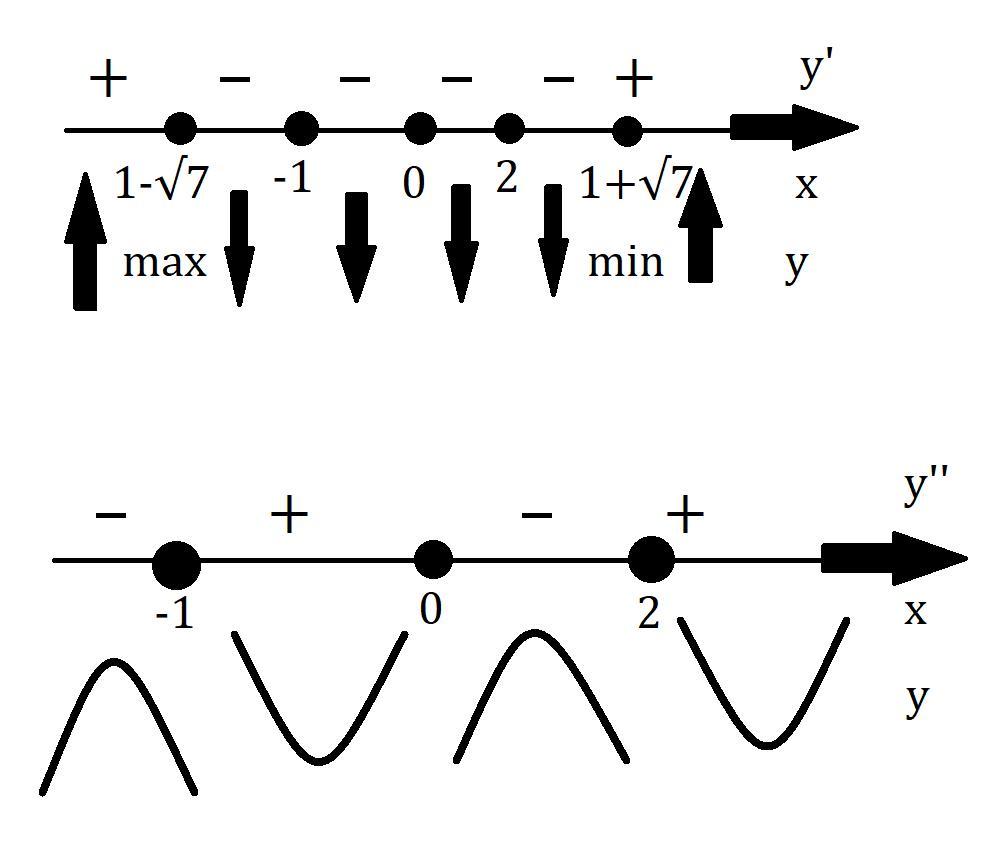
4. Исследование с первой производной:
Cм. внизу.
5. Исследование с второй производной:
Выражение в скобках в числителе всегда положительное и не равняется нулю, см. внизу.
6. Уравнение асимптот:
Уравнения наклонных асимптот обычно ищут в виде y = kx + b. По определению асимптоты:
Находим коэффициент k:
Находим коэффициент b:
Получаем уравнение наклонной асимптоты: у=x+2
Найдем вертикальные асимптоты. Для этого определим точки разрыва:
Находим переделы в точке x=-1
Это точка разрыва II рода и является вертикальной асимптотой.
Находим переделы в точке x=2
Это точка разрыва II рода и является вертикальной асимптотой.
Приложения:
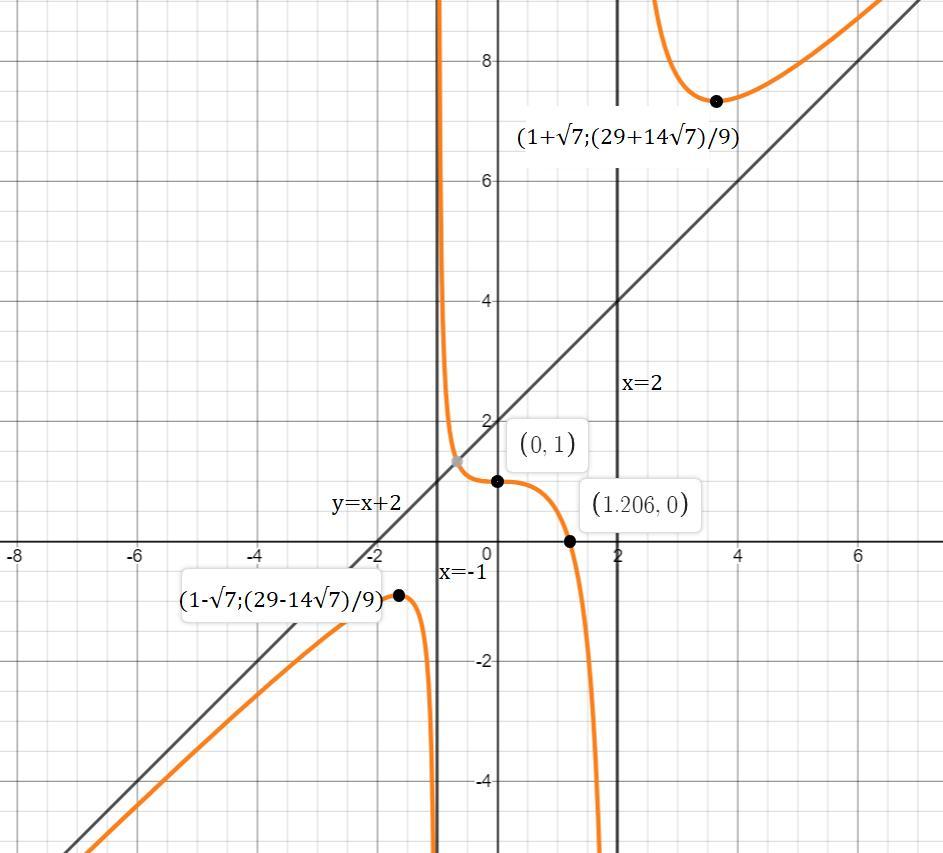
Ответ дал:
0
А понял
Ответ дал:
0
В этой точке функция определенна, наклонная асимптота для тех х, которые стремятся в бесконечность
Ответ дал:
0
спасибо
Ответ дал:
0
но почему точка пересечения не "черная" ?:)
Ответ дал:
0
Потому, что я её не выделил (все серые, когда наводишь чёрные), как бы зачем вам точка пересечения графика с наклонной асимптотой?
Вас заинтересует
2 года назад
3 года назад
9 лет назад
9 лет назад
10 лет назад
