Question

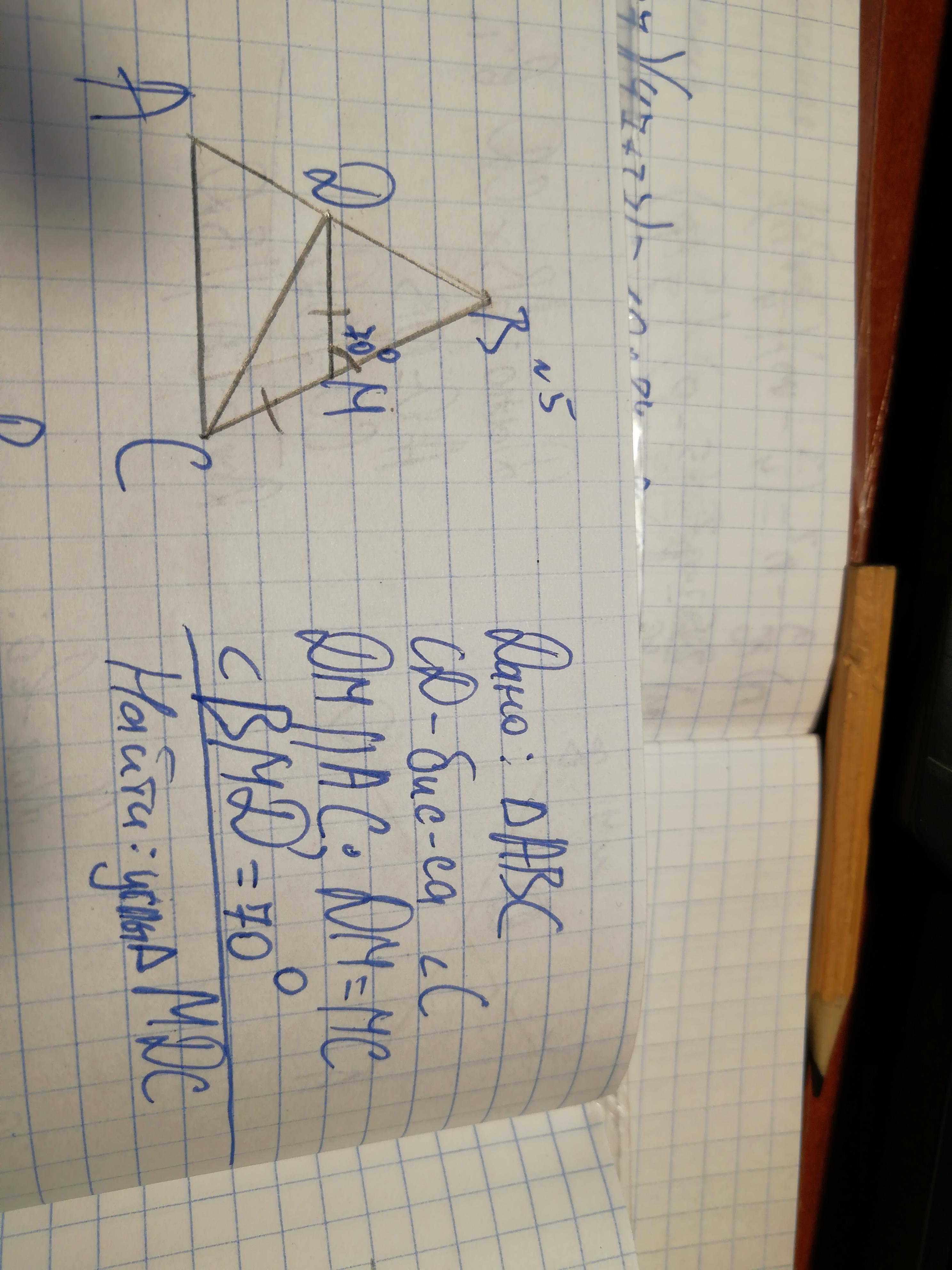
Дано треугольник ABC

CD биссектриса угла C

DM параллельна AC

DM=MC

угол BMD =70 градусам

Найти углы треугольника MDC

Answer 1

∠МДС=∠МСД, как углы при основании равнобедренного треугольника, посеольку ДМ=МС

∠ВМД-внешний угол при вершине М, и равен сумме двух внутренних углов, не смежных с ним, т.е. ∠МДС и ∠МСД, но они равны между собой .поэтому каждый равен по 35°

Ответ 35°

Answer 2

второй способ. Так как СД -биссектриса угла С, то угол ДСА равен углу ДСМ, а углы ВМД и ВСА равны, как соответственные при параллельных прямых ДМ и АС и секущей ВС, значит, угол ВСА тоже равен 70°, тогда его половина 35°, тогда и искомый угол МДС равен 35°, так как углы при основании равнобедренного треугольника равны. А треугольник МДС равнобедренный по условию. Ведь ДМ = МС. ВСЕ ПОНЯТНО? ЕСЛИ ОСТАЛИСЬ ВОПРОСЫ, задавайте. отвечу. Удачи.

Answer 3

Да, всё понятно, СПАСИБО ВАМ БОЛЬШОЕ!

Answer 4

Вам тоже спасибо за оценку. Удачи.