Найдите диагональ равнобокой трапеции основания которой равны 20 и 12 см , а диагонали перпендикулярны боковым сторонам
Ответы
Ответ дал:
0
Ответ:
Пошаговое объяснение:
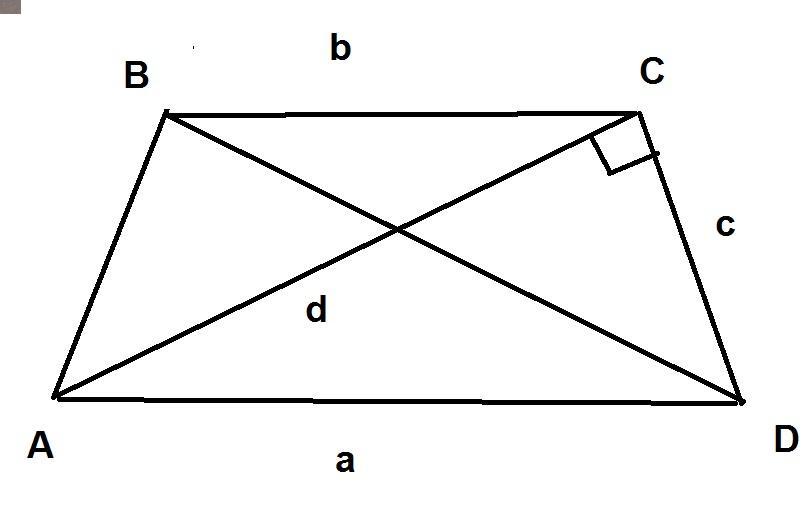
обозначим нижнее основание a
верхнее основание b
диагональ d
боковую сторону с
по формуле диагонали равнобокой трапеции d²=c²+ab
так как диагональ ⊥ боковой стороне то треугольник ACD прямоугольный к нему можно применить теорему Пифагора
квадрат гипотенузы = сумме квадратов катетов
катеты c и d, гипотенуза a
по теореме Пифагора a²=с²+d² объединим эти уравнения в систему
d²=c²+ab
a²=с²+d²
выразим с² из обоих уравнений
с²=d²-ab
c²=a²-d² приравняем правые части
d²-ab=a²-d² ; 2d²=a²+ab ; d²=(a²+ab)/2=(20²+20*12)/2=(400+240)/2=320
d=√320=√(64*5)=8√5
Приложения:
Вас заинтересует
2 года назад
2 года назад
3 года назад
3 года назад
9 лет назад
9 лет назад