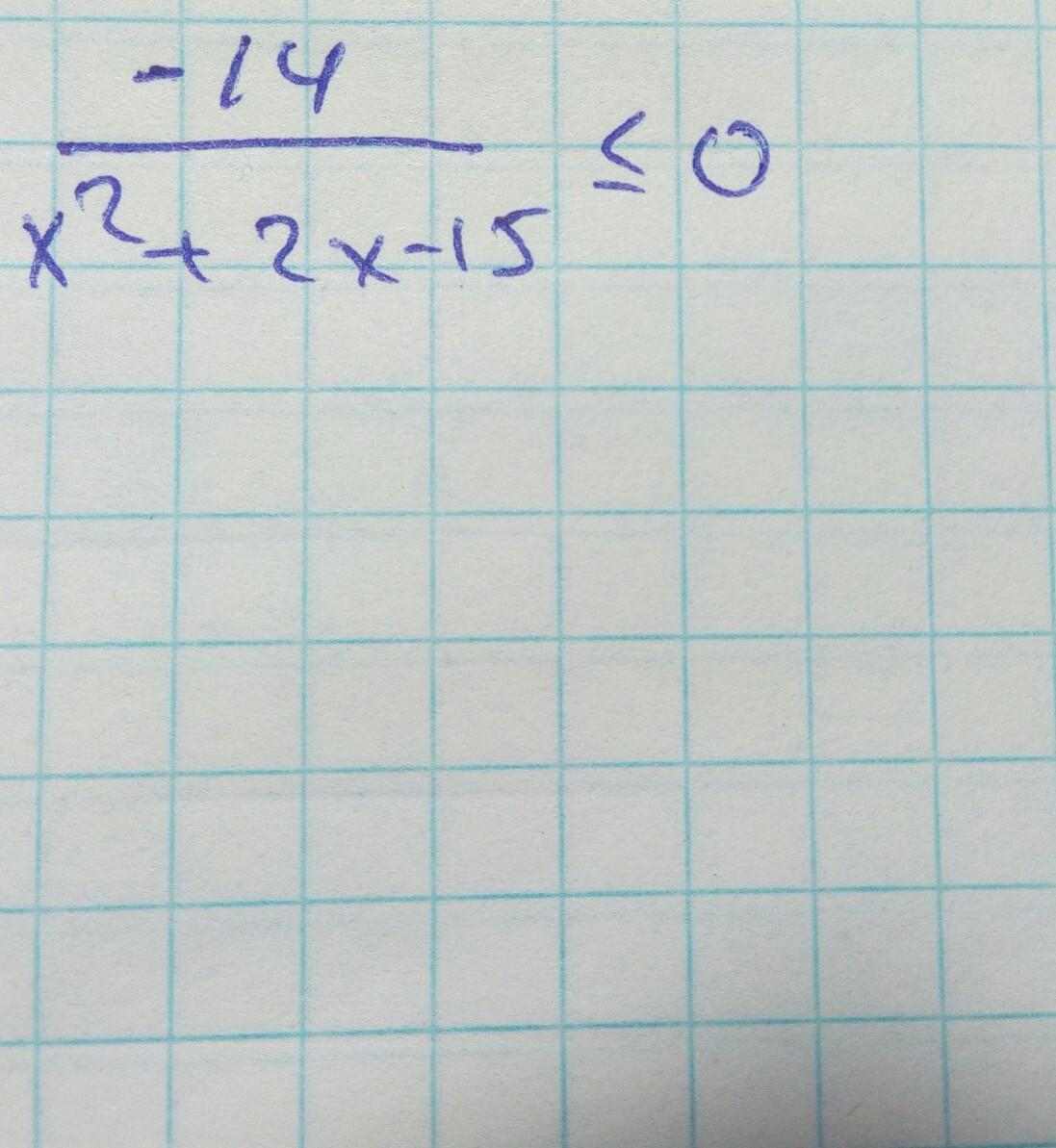Question

с объяснениями, пожалуйста
забыл, как делать :D​

Answer 1

Ответ:x ∈ (-∞ ; -5) ∪ (3; +∞)

Пошаговое объяснение:

1) Разложим знаменатель, для этого решим уравнение:

$x^{2} +2x-15=0\D=2^{2} +4*15=64=8^2\x 1=frac{-2+8}{2} =3\x2=frac{-2-8}{2}=-5$

кв. трехчлен  приобретает вид:

(x-3)(x+5)

дробь:

$frac{-14}{(x-3)(x+5)} leq 0$

справа ноль, значит можем делать равносильный переход, но учитываем, что на ноль делить нельзя, значит x≠-5 и x≠3

<=>

$-14(x-3)(x+5)leq 0$

разделим на -14, получим

(x-3)(x+5)>=0

далее, подключаем метод интервалов

отмечаем точки 3 и -5 на оси, тк учитываем ОДЗ , то точки будут выколотые (при них знаменатель обращается в ноль), несмотря на <=0.

расставляем знаки на промежутках знакопостоянства получаем

(плюс)------(-5)------(минус)----(3)---(плюс)--->x

тк на промежутке до -5 и после 3 знак положительный, это то, что нам нужно

x ∈ (-∞ ; -5) ∪ (3; +∞)

Answer 2

Выручил, спасибо!