Математики,які ще не сплять. Допоможіть!
Обчисліть похідні за допомогою логарифмічного диференціювання
Приложения:
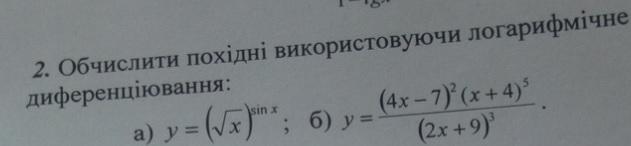
Ответы
Ответ дал:
0
a)
б)
Ответ дал:
0
Дякую ви просто були моя надія!!!!!Спасибі ВАММММ!!!!!!
Вас заинтересует
2 года назад
2 года назад
3 года назад
9 лет назад
9 лет назад