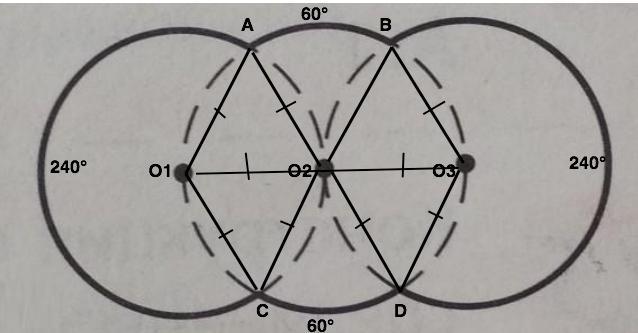
Фигура, изображенная на рисунке, построена из частей трех равных окружностей радиуса R. окружность, расположенная в средине, проходит через центры двух других окружностей. чему равен периметр выделенной фигуры?
Ответы
Ответ: 10πR/3
Пошаговое объяснение: Формула длины окружности 2πR. Полная градусная мера окружности 360°. Длина дуги, содержащей один градус, равна πR:180°
Обозначим центры окружностей: левой О₁, средней О₂ правой О₃, верхние точки пересечения А и В, нижние – С и D. Соединив точки пересечения окружностей, получим равносторонние треугольники, т.к. их стороны - равные радиусы равных окружностей. ⇒
Вписанные углы ∠АО₂С=∠ВО₂С=2•60°=120°. Полная окружность содержит 360°. Внешние дуги АС=ВD=360°-120°=240°. Меньшие верхняя и нижняя дуги АВ и СD равны по 60°, т.к. центральные углы при О2 равны по 60°. Периметр данной фигуры содержит дуги, суммарная градусная мера которых содержит 2•240-°+2•60°=600°.
Из найденной выше длины дуги 1° длина периметра фигуры Р=600°•πR/180°=10πR/3