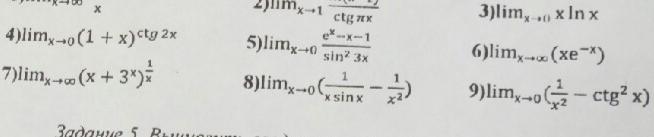Ответы
Ответ дал:
0
Пусть
Логарифмируем
Находим
Применяем правило Лопиталя:
sinx~x при х →0;
ln(1+x)~x при х →0
Значит,
Пусть
Логарифмируем
Находим
Применяем правило Лопиталя
Ответ дал:
0
https://znanija.com/task/32005504 , помогите пожалуйста 25 б с алгеброй
Вас заинтересует
3 года назад
9 лет назад
10 лет назад
10 лет назад