Question

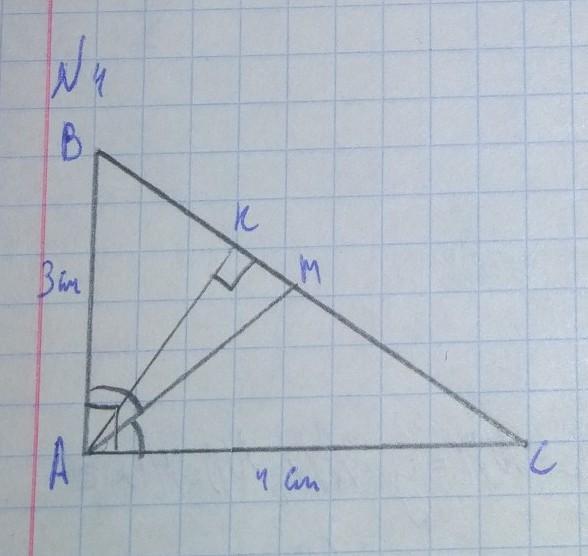
В треугольнике АВС с прямым углом А проведены высота AК и биссектриса АМ. Найдите КМ, если АВ=3 см АС =4 см. (см.чертеж)​

Answer 1

1. По теореме Пифагора из ΔABC найдём BC:

$BC=sqrt{AC^2+AB^2}=sqrt{16+9}=sqrt{25}=5cm$

2. SΔABC можно найти разными способами:

$SDelta ABC= frac{1}{2}AB cdot AC = frac{1}{2}cdot 3 cdot 4 = 6 cm^2$

$SDelta ABC= frac{1}{2}BC cdot AK=frac{5}{2} AK$

Откуда можно найти AK:

$frac{5}{2}AK=6\ 5AK=12\ AK=frac{12}{5}cm$

3. По теореме Пифагора из ΔABK найдём BK:

$BK=sqrt{AB^2-AK^2}=sqrt{9-frac{144}{25}}=sqrt{frac{225-144}{25}}=sqrt{frac{81}{25}}=frac{9}{5}cm$

4. $KC=BC-BK=5-frac{9}{5}=frac{25-9}{5}=frac{16}{5}cm$

5. Пусть x=KB, тогда $BM=frac{9}{5}+x,MC=frac{16}{5}-x$

Используя свойство биссектрисы треугольника, составим уравнение:

$frac{AC}{MC}=frac{AB}{BM}\ \ frac{4}{frac{16}{5}-x}=frac{3}{frac{9}{5}+x}\ \ frac{4}{frac{16-5x}{5}}=frac{3}{frac{9+5x}{5}}\ \ frac{4cdot 5}{16-5x}=frac{3cdot 5}{9+5x}\ \ frac{4}{16-5x}=frac{3}{9+5x}\ \ 4(9+5x)=3(16-5x)\ 36+20x=48-15x\ 35x=12\ \ KM=x=frac{12}{35}cm$

$OTBET: frac{12}{35}cm$

Answer 2

Только AK можно проще найти, по свойству пропорциональных отрезков

Answer 3

И по сути AK тут и не нужно

Answer 4

Дело Ваше:) Решений то много у задачи

Answer 5

Я просто говорю тем, кто будет просматривать. Мне бы на ваше решение сказали:"не рационально" и поставили бы 2