Question

Срочно!

Определите общее сопротивление участка электрической цепи между точками AB, которая состоит из бесконечного количества одинаковых резисторов. Сопротивление каждого резистора равно 2 Ом​

Answer 1

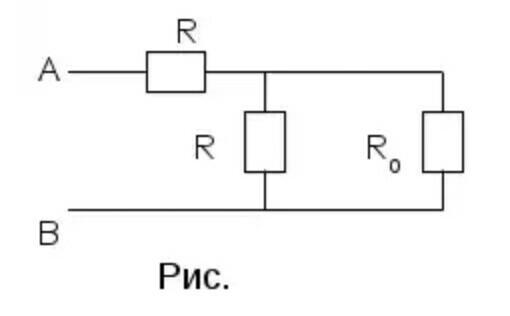
Выделим повторяющийся элемент схемы. В данном случае таким элементом будет такая схема (рис. ) Так как цепочка бесконечна, то при удалении первого элемента сопротивление схемы не изменится. Обозначим общее сопротивление цепочки через RО. Тогда, при удалении первого элемента сопротивление оставшейся цепочки будет также RО, и вместо бесконечной цепочки можно рассматривать такую схему (рис. )

Сопротивление между точками А и В такой схемы:

RAB=R+(R*RO)/(R+RO)

Так как RAB=RO

R=R+(R*RO)/(R+RO)

Решаем полученное уравнение относительно неизвестной величины RО. После приведения к общему знаменателю и группировки подобных членов получим квадратное уравнение

R^2O-RRO-R^2=0

Решая относительно RО, получим

RO=

$frac{r}{2} frac{ + }{} sqrt{ frac{ {r}^{2} }{4} + {r}^{2} }$

RO=

$frac{r}{2} (1 + sqrt{5} )$

Отрицательный корень отбрасываем, т.к. RО>0.

Подставляя значение R=2 Ом, получаем ответ

$1 + sqrt{5}$