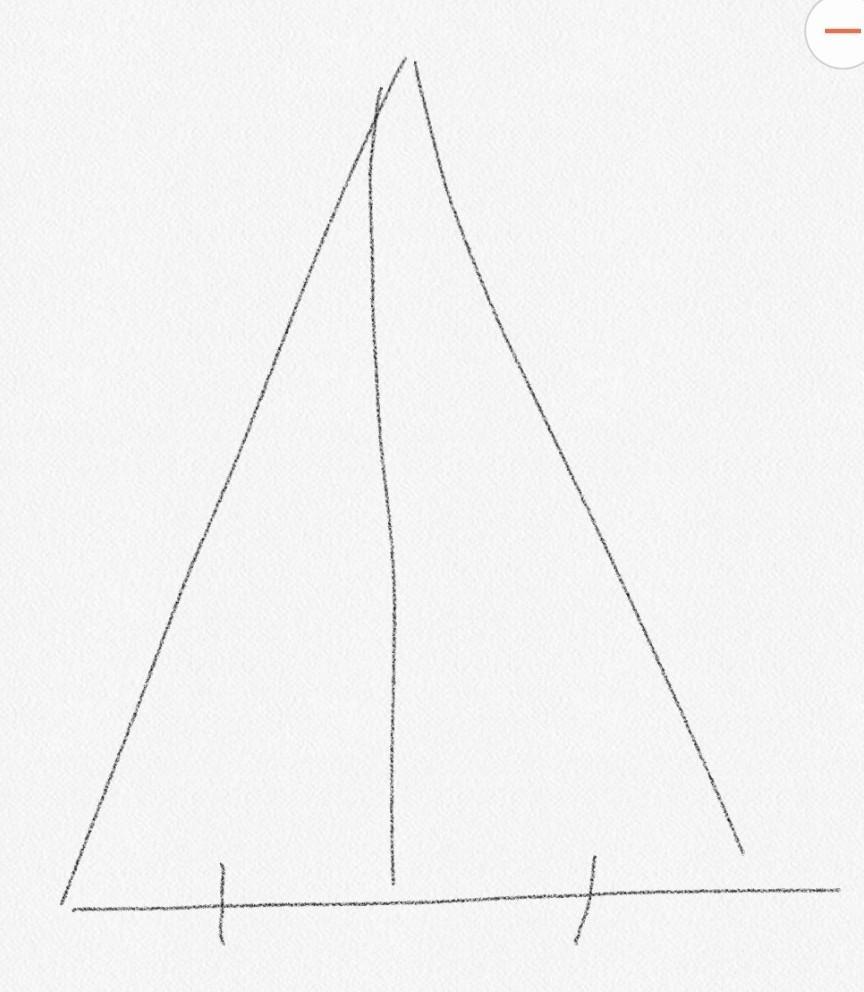Ответы
Ответ дал:
0
Решение на фото!
_______________________________
удачи))
Понравилось решение?Жми ЛУЧШИЙ!)
Приложения:
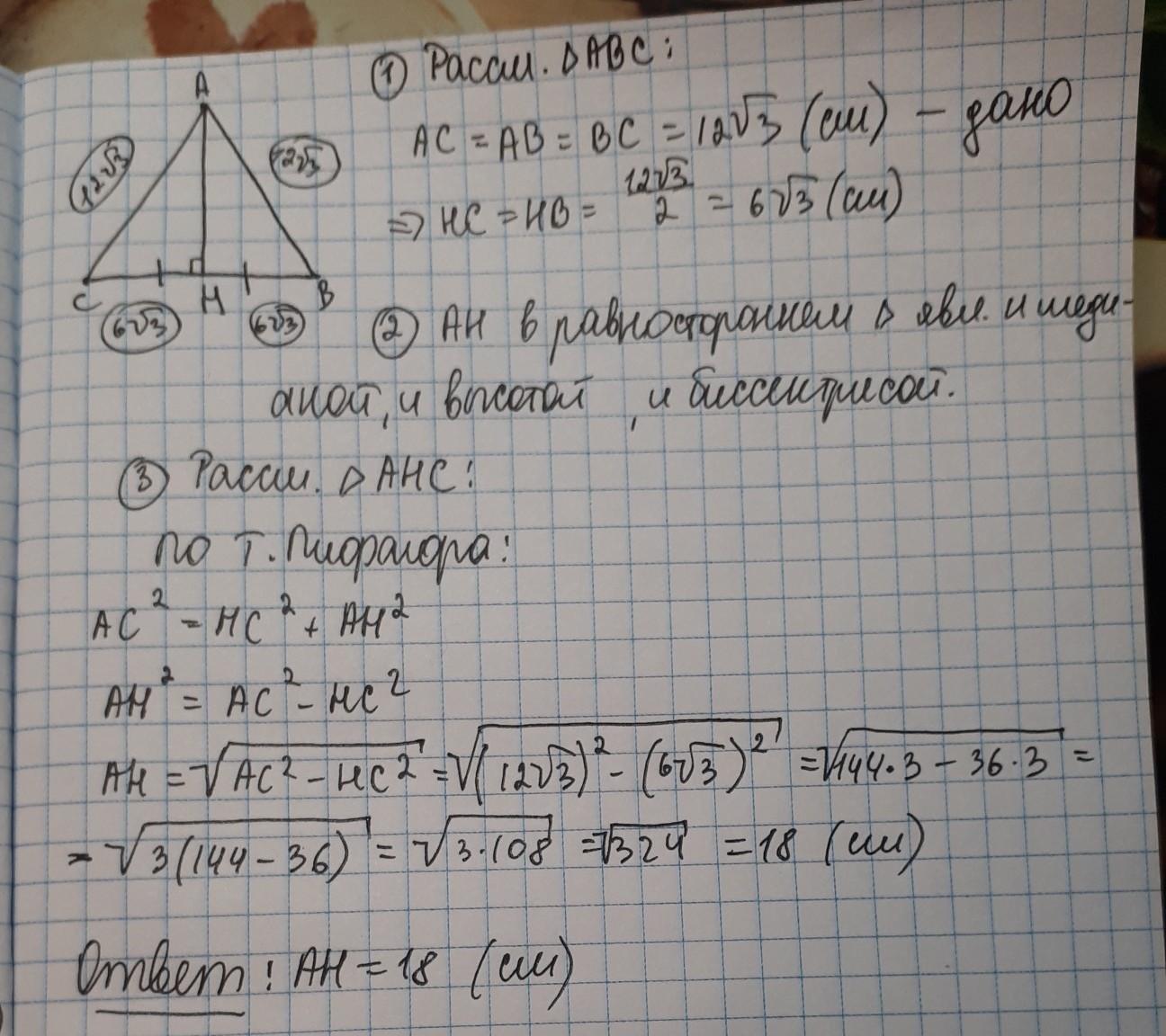
Ответ дал:
0
т. к. треугольник расносторонний, то все углы в нем по 60 градусов, значит, проведенная медиана является еще и бессиктрисой, следовательно, угол АВН(угол В-наверху, а ВН-медиана) равен 30 градусов.
Половинка основания равна

Треугольник АВН - прямоугольный, т.к. проведенная медиана является еще и высотой. Значит, по т. Пифагора мы можем найти ВН:

Ответ: 18.
Половинка основания равна
Треугольник АВН - прямоугольный, т.к. проведенная медиана является еще и высотой. Значит, по т. Пифагора мы можем найти ВН:
Ответ: 18.
Приложения:
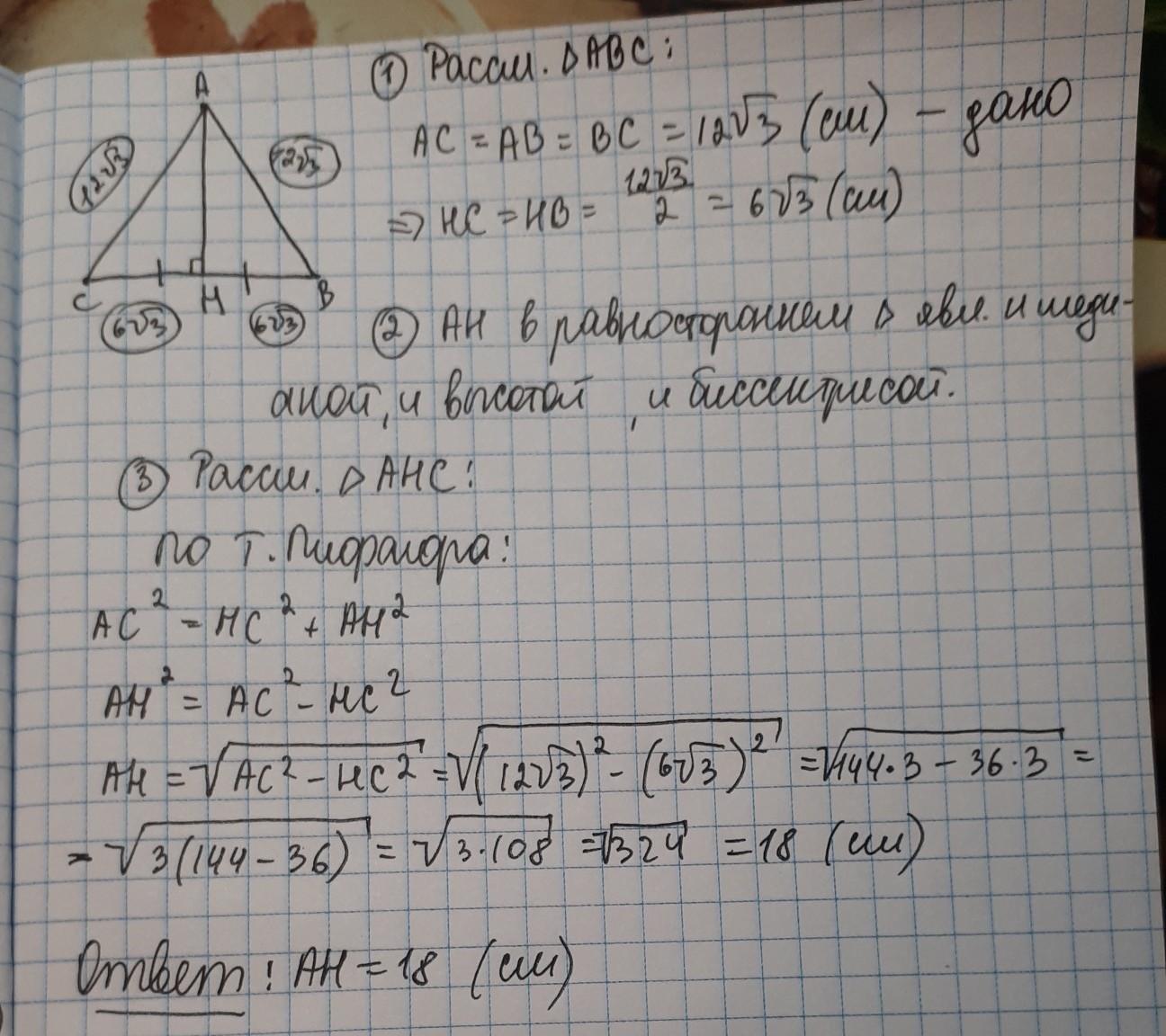
Ответ дал:
0
высота (медиана, биссектриса) равностороннего треугольника равна половине произведения длины стороны на квадратный корень из 3. подставляем в формулу известную сторону и решаем все задание в одно действие!!! это же надо так нагородить в решении!!
Вас заинтересует
2 года назад
2 года назад
3 года назад
9 лет назад
9 лет назад
10 лет назад