Question

ДАМ ОЧЕНЬ МНОГО БАЛЛОВ ЗА ЭТО ЗАДАНИЕ!!!!!!!!!!!!!!!!!!!!!!!! ПОМОГИТЕ СРОЧНО С РИСУНКОМ!!!!!!!!!!!!!!!!!!!!
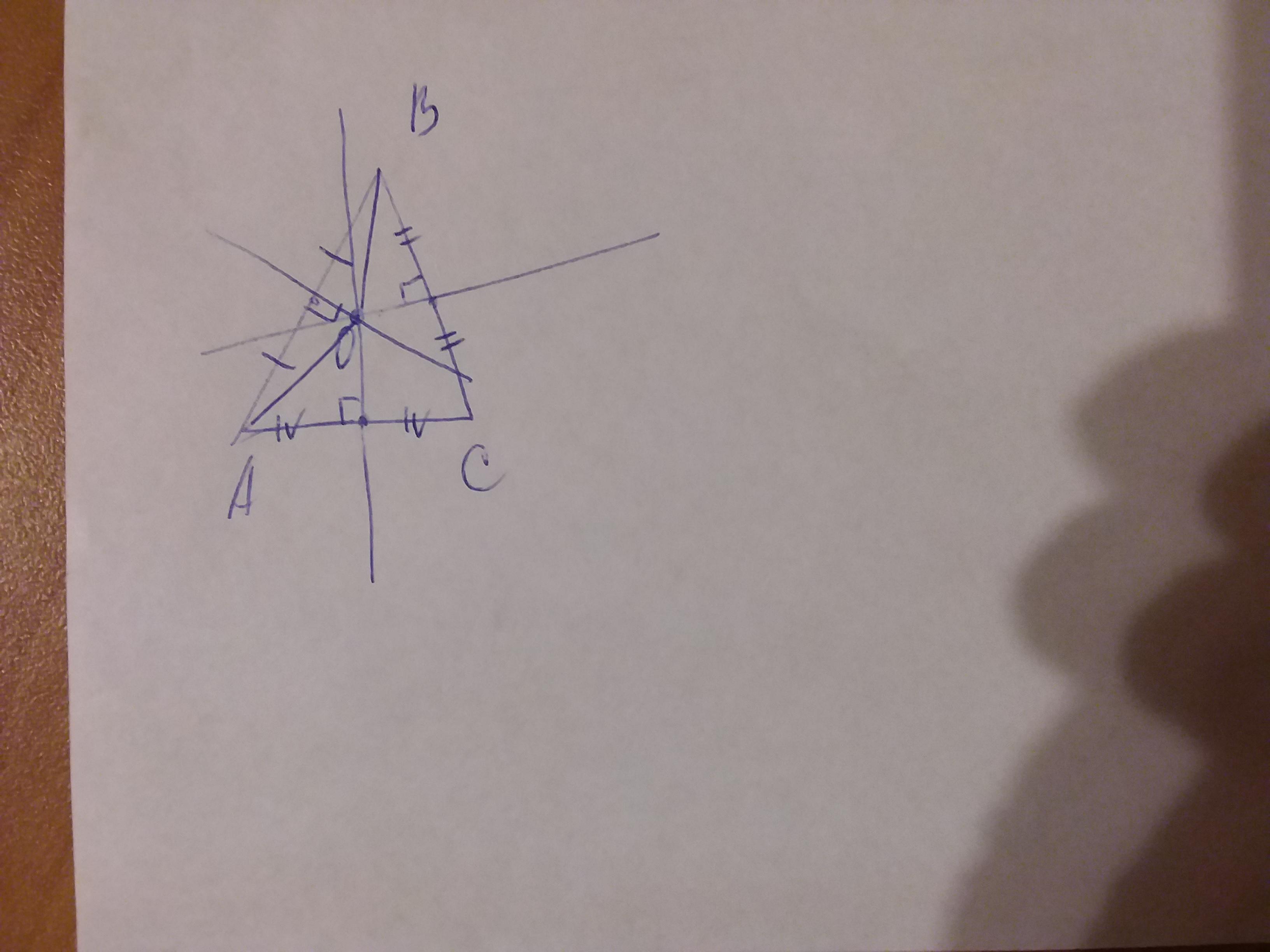
Серединные перпендикуляры треугольника АВС пересекаются в точке О.

Найдите длину стороны АВ, если ОА = 8 см, ∠АОВ = 60градусов.

Answer 1

точка пересечения серединных перпендикуляров-центр описанной окружности,т.е.ОВ=ОА=8см.

по т.косинусов АВ²=ОВ²+ОА²-2*ОА*ОВ*cos 60°=64+64-2*64*1/2=128-64=64

АВ=√64=8

или так:∠ОАВ=∠ОВА=(180°-60°):2=60-как углы при основании р/б треугольника АОВ,т.е.,ΔАОВ-равносторонний,и АВ=ОА=ОВ=8см.

Answer 2

спс