Найти производную (сокращать не нужно , жел.обьяснить по пунктам )
Буду признателен .
(sin x/4 - cos x/4 ) ^ 2
f ' (x) =
Ответы
Ответ дал:
0
решение на фото ниже. задавайте вопросы если не понятно
Приложения:
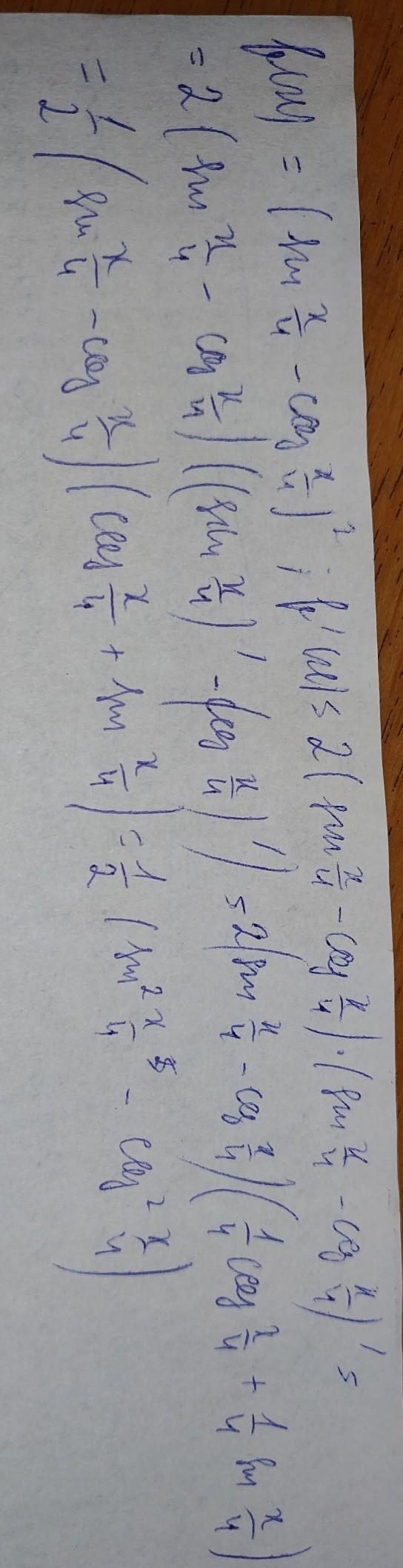
Ответ дал:
0
ничего не ясно
Ответ дал:
0
а вы осведомлены о том, что такое производная?
Ответ дал:
0
да осведомлен
Ответ дал:
0
здесь используется правило нахождения производной сложной функции
Ответ дал:
0
2 ряд в конце , почему там стоит 1/4 cos x/4 + 1/4 sin x/4 . Если прзв-ние sin 1/4 просто сos 1/4 а сos 1/4 это - sin 1/4 ) не пойму я этот момент
Ответ дал:
0
Ответ: В первую очередь находим производную от степени. Далее расписала подробно
Приложения:
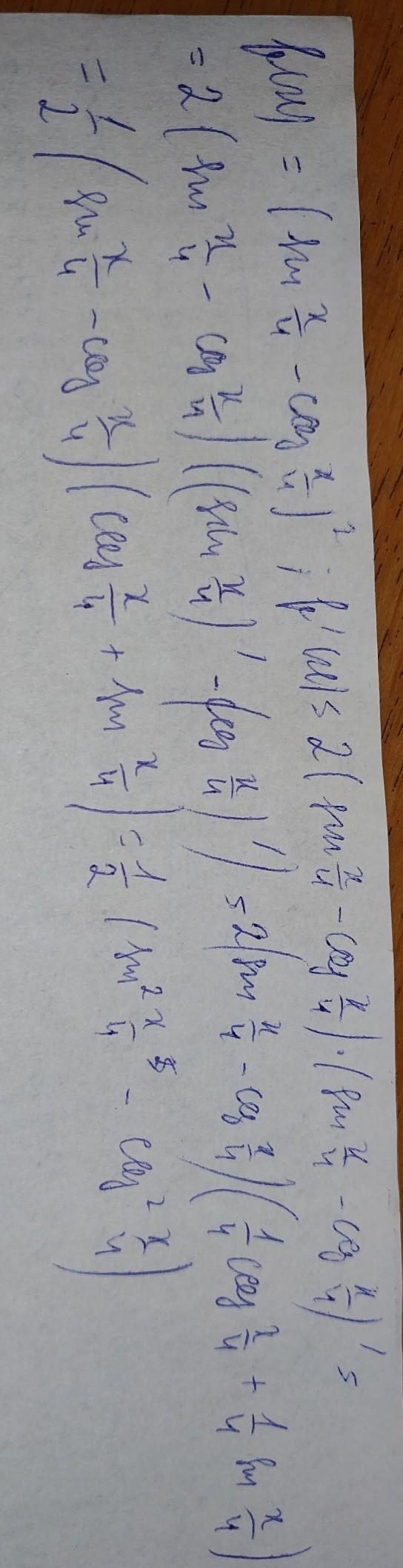
Ответ дал:
0
вот тут все ясно , спасибо .
Вас заинтересует
2 года назад
2 года назад
3 года назад
9 лет назад
9 лет назад